itmo_conspects

Лекция 10. Кластеризация

Кластеризация, то есть разделение элементов выборки по схожести, является видом так называемого обучения без учителя - мы изначально не знаем, какие признаки имеют наши

Кластеризацию не стоит путать с уменьшением размерности данных: кластеризация - это поиск общих групп, а уменьшение размерности - поиск нового представления данных

Можно выделить 4 подхода:

1. Разделение, основанное на центах (Centroid-based partitioning clustering)
2. Кластеризация, основанная на плотности (Density-based clustering)
3. Иерархическая кластеризация (Hierarchical clustering)
4. Кластеризация, основанная на модели (Model-based clustering) - методы не всегда универсальные, поэтому они не будут здесь разбираться

Кластеризация, основанная на центрах

В методах, основанных на центрах, алгоритмы ищут центроиды - точки, которые описывают центры будущих кластеров

Центроид - это такая точка, сумма квадратов расстояний до точек в кластере минимальна

В методе $k$ средних (k-means):

• Случайным образом выбираются $k$ центроидов
• Для этих $k$ центроидов ищутся ближайшие точки из выборки, которые образуют кластеры
• Далее для этих кластеров ищутся новые центроиды
• Для этих центроидов пересчитываются кластеры и шаги повторяются

Алгоритм повторяется до тех пор, пока положение центроидов меняется

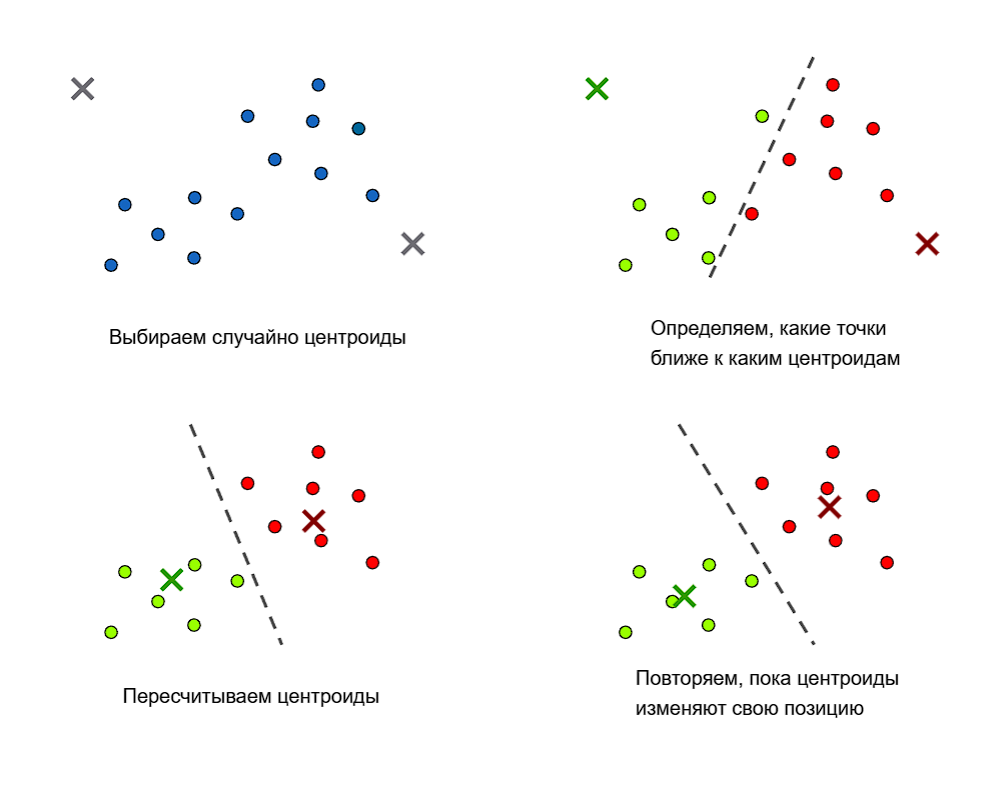
Выбор точек может быть таким:

• Случайным образом в пространстве
• Одними из точек выборки
• Или разбросаны так, что каждый центроид - эта точка из выборки, и центроиды находятся наиболее далеко от друг от друга - такой подход называется k-means++

Большим недостатком методов, основанных на центроидах, - это выбор числа кластеров $k$. Также методом $k$ средних плохо различаются кластеры невыпуклой формы

Кластеризация, основанная на плотностях

В методах, основанных на плотностях, другой подход. В них точки считаются кластерами, если они плотно (то есть близко) расположены

Популярным таким методом является DBSCAN (Density-Based Spatial Clustering of Applications with Noise, Основанная на плотности пространственная кластеризация для приложений с шумами) и работает так:

• Берется невыбранная точка
• Вокруг радиуса $\varepsilon$ считаются точки

• Если их больше определенного числа $\text{min\_samples}$, то считается, то они принадлежат одному кластеру

  Точка, вокруг которой есть $\text{min\_samples}$ точек, считается основной (core point). Точка, вокруг которой меньше $\text{min\_samples}$ точек, но она принадлежит кластеру, считается пограничной (border point)

• Если точка не принадлежит какому-либо кластеру, то она считается выбросом

Наивно DBSCAN работает за квадрат (считаем все расстояния между точками), однако с помощью деревьев и индексов можно получить асимптотику лучше

Иерархическая кластеризация

Иерархическая кластеризация - это метод кластеризации, который строит иерархию кластеров в виде дерева, которое называется дендрограммой. Такие методы делятся на агломеративные (от меньших кластеров к большим) и дивизивные (от больших к меньшим)

Чаще всего используется агломеративный подход, который работает так:

• Каждая точка считается кластеров
• Вычисляются расстояния между кластерами
• Два ближайших кластера сливаются в один
• Расстояния пересчитываются
• Алгоритм повторяется, пока не будет один больший кластер

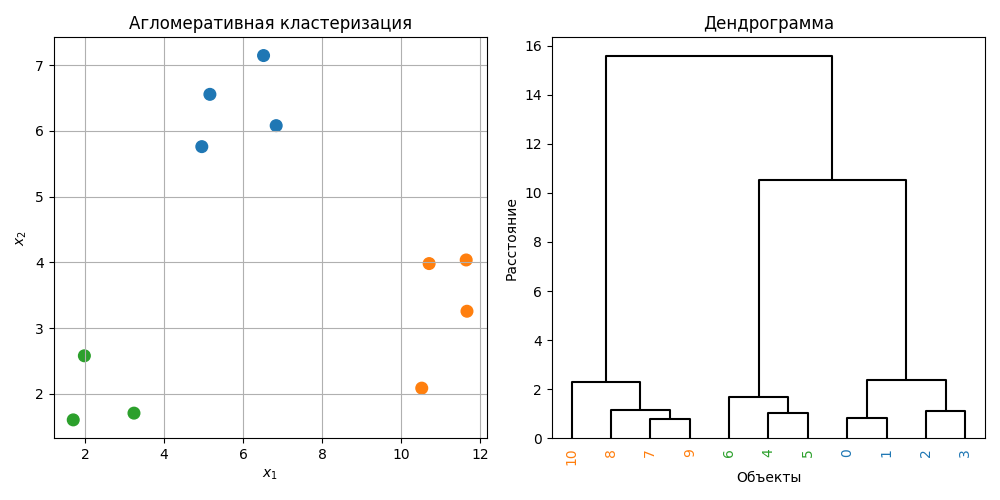
Если расстояния между точками тривиально вычисляется, то расстояния между кластерами (так называемый linkage) можно считать разными способами

• Метод одиночной связи (Single linkage): расстояния между кластерами - это расстояние между ближайшими точками кластеров
• Метод полной связи (Complete linkage): расстояния между кластерами - это расстояние между дальнейшими точками кластеров
• Метод средней связи (Average linkage или Pair-group method using arithmetic mean): расстояния между кластерами - это среднее расстояние между всеми попарно различными точками, может быть взвешенным
• Центроидный метод (Centroid linkage или Pair-group method using the centroid average): расстояния между кластерами - это расстояние между центроидами
• Метод Уорда (Ward linkage): расстояния между кластерами - это прирост дисперсии расстояний между точками кластеров и соответствующего центроида $\displaystyle \Delta = \sum_{x_i \in A + B} (x_i - \overline{x})^2 - \sum_{x_i \in A} (x_i - \overline{a})^2 - \sum_{x_i \in B} (x_i - \overline{b})^2$

Также сами расстояния между точками можно вычислять по-разному: евклидово, манхеттенское, косинусное и так далее

Иерархическая кластеризация позволяет взглянуть, как кластеры друг к другу относятся, однако:

• Требует $O(n^2)$ памяти и $O(n^3)$ времени
• Не устойчив к шуму и большим выбросам

Код примера - machlearn_agglomerative_clustering.py

---

Методы можно комбинировать - так появился HDBSCAN (Hierarchical DBSCAN). В нем:

• Вводится метрика расстояния взаимной достижимости (Mutual reachability distance) $\mathrm{mreach}(x, y) = \max(\mathrm{kdist}(x), \mathrm{kdist}(y), \mathrm{dist}(x, y))$, где $\mathrm{kdist}(x)$ - расстояния от точки $x$ до $k$-ого ближайшего соседа ($k$ - это $\text{min \_ samples}$), $\mathrm{dist}(x, y)$ - расстояния между точками $x$ и $y$
• Строится полный взвешенный граф, где вес ребра - это $\mathrm{mreach}(x, y)$
• Строится минимальное остовное дерево, используя алгоритмы Краскала или Прима. Такое дерево считается одним большим кластером
• Далее удаляем ребра с наибольшим $\mathrm{mreach}(x, y)$, тем самым разбивая кластеры на два и получая иерархию

Здесь не используется параметр $\varepsilon$, что позволяет хорошо выделять кластера с разными плотностями. Однако, можно задать $\text{min \_ cluster \_ size}$ - минимальный размер устойчивого кластера

Устойчивыми кластерами считаются те, которые долго не распадаются. Для этого вводится метрика $\displaystyle \mathrm{Stability}(C) = \sum_{i \in C} (\lambda_{i} - \mu_{C})$, где $\mu_{C} = \frac{1}{\mathrm{mreach}(x, y)}$ - обратное к весу ребра, удаление которого привело к появлению кластера, а $\lambda_{i} = \frac{1}{\mathrm{mreach}(x_i, x_j)}$ - обратное к весу ребра, удаление которого привело к отделению $i$-ой точки

Для такой иерархии кластеров

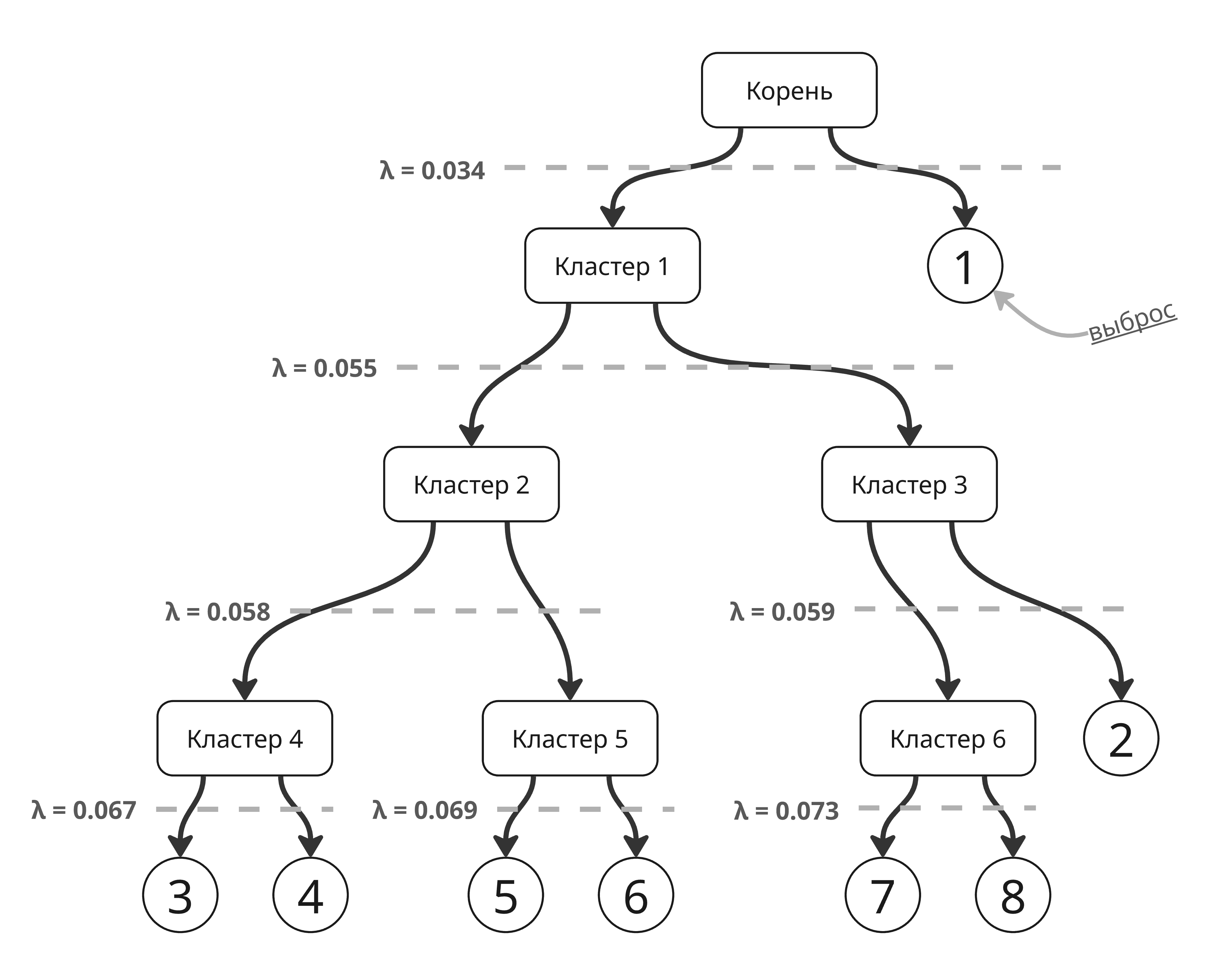
стабильность кластера 1 определяется как сумма $(0.067 - 0.034) + (0.067 - 0.034) + (0.069 - 0.034) + (0.069 - 0.034) + (0.073 - 0.034) + (0.073 - 0.034) + (0.059 - 0.034) = 0.239$ 😲

А стабильность кластера 3 равна $(0.059 - 0.055) + (0.073 - 0.055) + (0.073 - 0.055) = 0.04$

Дополнительная информация о HDBSCAN: https://lanselin.github.io/introbook_vol1/HDBSCAN.html

Метрики кластеризации

Чтобы оценить, насколько хороша кластеризация выборки, можно использовать следующие метрики:

• Оценка силуэта (Silhouette score)

  Для $i$-ой точки в кластере определим $\displaystyle a(i) = \frac{1}{\vert C_i \vert - 1} \sum_{x_j \in C_i, i \neq j} \mathrm{dist}(x_i, x_j)$ - среднее расстояние от выбранной точки до остальных в том же кластере

  Также определим $\displaystyle b(i) = \min_j \frac{1}{\vert C_j \vert} \sum_{x_k \in C_j} \mathrm{dist}(x_i, x_k)$ - минимальное из средних расстояний от выбранной точки до точек другого кластера

  Тогда оценка силуэта для точки считается равной как $s(i) = \frac{b(i) - a(i)}{\max(b(i), a(i))}$

  Для кластера из одной точки $s(i) = 0$. Из определения видно, что $s(i) \in [-1; 1]$

  Чем больше оценка силуэта, тем наиболее правильно точка отнесена к кластеру

  На основе этого можно построить график оценок силуэта (Silhouette plot):

  

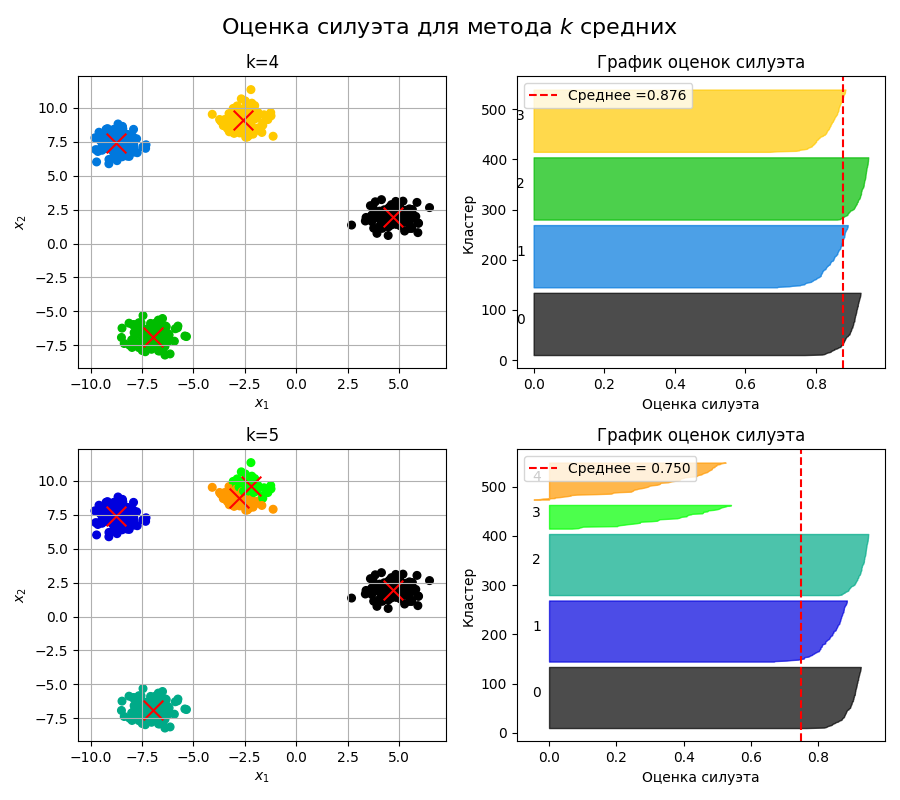
  Здесь красная пунктирная линия - среднее из оценок для всех точек. Кластеры считаются хорошо разделенными, если максимум оценки силуэта точек внутри кластера больше этого среднего

  Код примера - machlearn_silhouette_plot.py

• Оценка или индекс DBCV (Density-Based Clustering Validation)

  Оценка DBCV считается так:

  1. Строится минимальное остовное дерево, как в HDBSCAN
  2. Обозначим остов внутри кластера $C_i$ как $T_i$
  3. Вычисляется значение Density Sparseness of a Cluster: $\displaystyle \mathrm{DSC}(C_i) = \max_{(x_i, x_j) \in T_i} \mathrm{mreach}(x_i, x_j)$ - максимальный вес ребра остова
  4. Вычисляется значение Density Separation of a Pair of Clusters: $\displaystyle \mathrm{DSBC}(C_i, C_j) = \min_{x_i \in C_i, x_j \in C_j} \mathrm{mreach}(x_i, x_j)$ - минимальный вес ребра между точками разных кластеров
  5. Далее $\mathrm{DBCV} = \sum_i \frac{\vert C_i \vert}{n} \frac{\min_{i \neq j} \mathrm{DSPC}(C_i, C_j) - \mathrm{DSC}(C_i)}{\max(\min_{i \neq j} \mathrm{DSPC}(C_i, C_j), \mathrm{DSC}(C_i))}$

  Метрика DBCV высока, если кластеры состоят из плотно расположенных точек, и учитывает более сложную форму кластеров, чем оценка силуэта

  

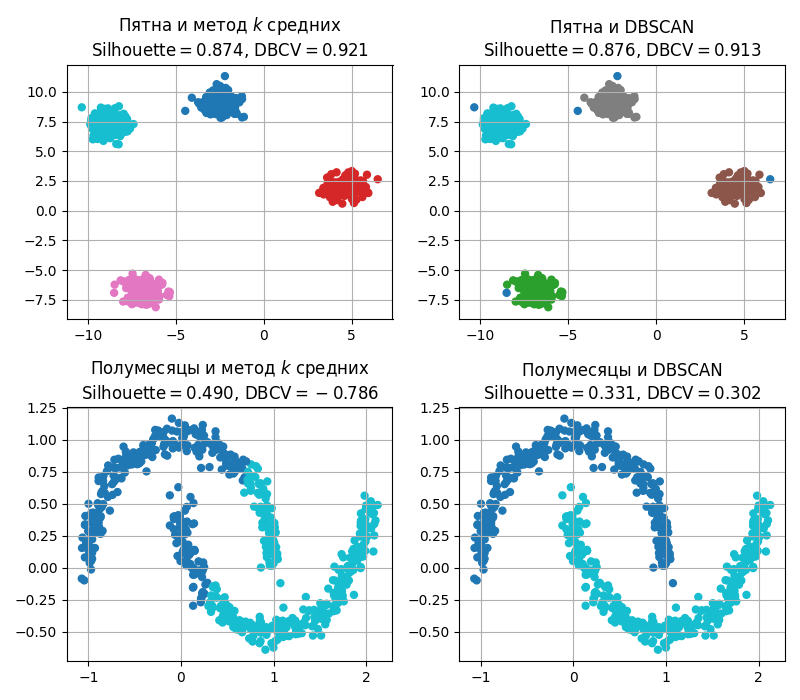
  Код примера - machlearn_silhouette_dbcv.py

  Статья про DBCV: https://www.researchgate.net/publication/260333211_Density-Based_Clustering_Validation

• Оценка Калински-Харабаша (или критерий дисперсионного отношения, Variance Ratio Criterion, VRC)

  Оценка Калински-Харабаша вычисляется так: $\mathrm{CH} = \frac{\mathrm{BCSS}}{k - 1} \frac{n - k}{\mathrm{WCSS}}$, где $k$ - число кластеров, $n$ - размер выборки

  Здесь $\displaystyle \mathrm{BCSS} = \sum_{i = 1}^k n_i | c_i - c |^2$ - межкластерная сумма квадратов расстояний (Between-Cluster Sum of Squares), где $c_i$ - центроид $i$-ого кластера, $n_i$ - размер $i$-ого кластера, $c$ - среднее всех точек из выборки

  $\displaystyle \mathrm{WCSS} = \sum_{i = 1}^k \sum_{x \in C_i} | x - c_i |^2$ - внутрикластерная сумма квадратов расстояний (Within-Cluster Sum of Squares), где $c_i$ - центроид $i$-ого кластера, $x$ - точка из $i$-ого кластера

• Метод локтя (Elbow method или Knee method)

  Метод локтя применяется для определения оптимального числа кластеров. Для этого:

  • Выбирается число кластеров
  • Точки кластеризуются в такое число кластеров
  • Вычисляется внутрикластерная сумма квадратов расстояний $\mathrm{WCSS} = \sum_{i = 1}^k \sum_{x \in C_i} | x - c_i |^2$, где $c_i$ - центроид $i$-ого кластера, $x$ - точка из $i$-ого кластера

  Далее данные наносят на график:

  

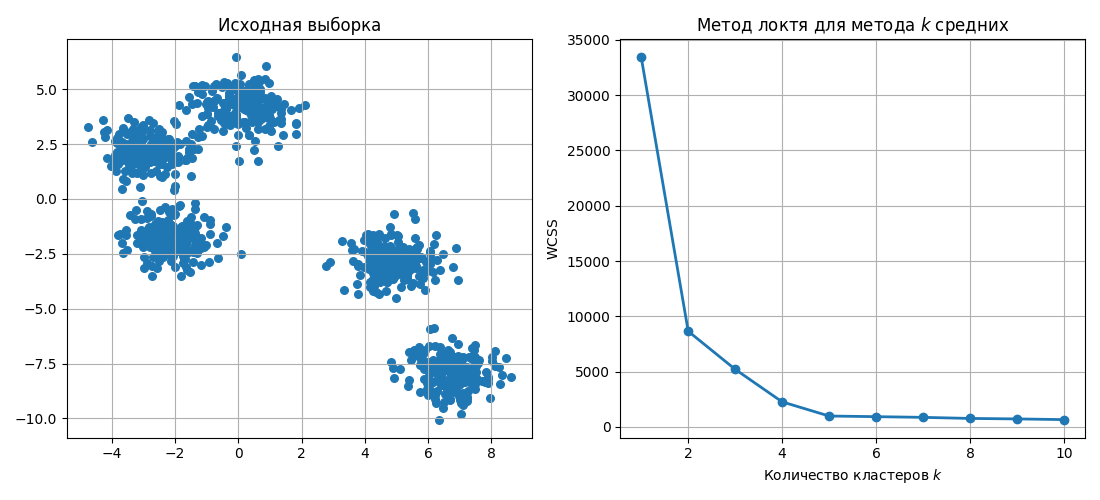
  $\mathrm{WCSS}$ при увеличении числа кластеров будет уменьшаться (так как в пределе один кластер - это одна точка, которая является центроидом кластера), однако после некоторого числа кластеров уменьшение будет не таким значимым

  Это число считается оптимальным для разбиения, для примера на картинке таковым является 5

  Код примера - machlearn_cluster_elbow_method.py

• Чистота кластеров (Purity)

  Если метки кластеров для точек заранее известны, то можно воспользоваться метрикой чистоты кластеров \(\mathrm{Purity}(C_k) = \frac{1}{\vert C_k \vert} \max_{c} \vert \{ x_i \in C_k \} \, \vert \, y_i = c \vert\)

  Для всех данных чистота определяется как взвешенное среднее: $\mathrm{Purity} = \frac{1}{n} \sum_{i = 1}^k \vert C_i \vert \mathrm{Purity}(C_i)$

• Удержание (Retention)

  Удержание - это доля объектов, которые остались в том же кластере при кластеризации с немного измененными объектами: $\mathrm{Retention} = \frac{1}{N} \sum_i I(y_i^{(1)} = y_i^{(2)})$

  Идея состоит в том, что при кластеризации с немного измененными параметрами (например, при изменении $\varepsilon$ в DBSCAN) объекты должны попадать в те же кластеры, а если кластеры сильно меняются, то выбранный метод кластеризации нестабилен на этих данных

This site is open source. Improve this page.