itmo_conspects
Лекция 8. Деревья, лес, бустинг
Закономерность $\varphi$ называется интерпретируемой, если:
- Она сформулирована естественным языком
- Зависит от небольшого числа параметров (от одного до семи)
Закономерность $\varphi$ называется информативной, если число истинно положительных результатов предсказаний \(p(x) = \vert \{ x_i \ \vert \ \varphi(x_i) = 1, y_i = c \} \vert\) максимально, а число ложноположительных результатов \(n(x) = \vert \{ x_i \ \vert \ \varphi(x_i) = 1, y_i \neq c \} \vert\) минимально
Пусть у нас есть закономерность, говорящая, при каких условиях погоды состоится матч по бейсболу:
| № | Погода | Температура | Влажность | Ветер | Можно играть |
|---|---|---|---|---|---|
| 1 | Солнечная | Жарко | Высокая | Слабый | ❌ Нет |
| 2 | Солнечная | Жарко | Высокая | Сильный | ❌ Нет |
| 3 | Облачная | Жарко | Высокая | Слабый | ✅ Да |
| 4 | Дождливая | Тепло | Высокая | Слабый | ✅ Да |
| 5 | Дождливая | Холодно | Средняя | Слабый | ✅ Да |
| 6 | Дождливая | Холодно | Средняя | Сильный | ❌ Нет |
| 7 | Облачная | Холодно | Средняя | Сильный | ✅ Да |
| 8 | Солнечная | Тепло | Высокая | Слабый | ❌ Нет |
| 9 | Солнечная | Холодно | Средняя | Слабый | ✅ Да |
| 10 | Дождливая | Тепло | Средняя | Слабый | ✅ Да |
| 11 | Солнечная | Тепло | Средняя | Сильный | ✅ Да |
| 12 | Облачная | Тепло | Высокая | Сильный | ✅ Да |
| 13 | Облачная | Жарко | Средняя | Слабый | ✅ Да |
| 14 | Дождливая | Тепло | Высокая | Сильный | ❌ Нет |
Закономерность можно представить в виде дерева решений:
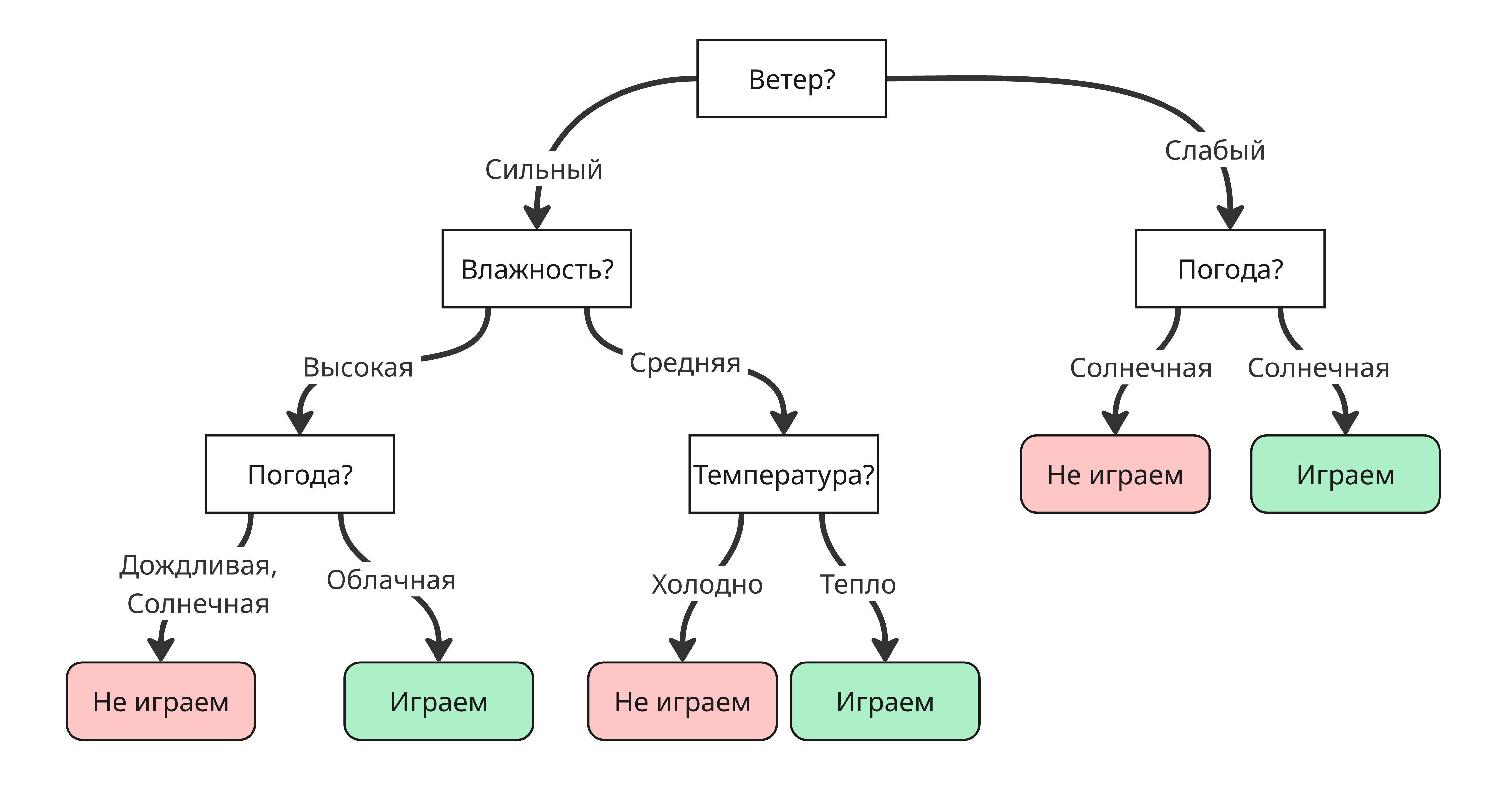
Такое дерево называется деревом решений - это дерево, для которого:
- Корень представляет начальное условие
- Ребра и соответствующие им ветви - это проверки условий по признакам
- Листья - это конечные решения (класс или число)
Для одного вопроса можно собрать множества деревьев решений, но нас интересуют оптимальные, то есть те, которые за меньшее число вершин прохода приходят к ответу. Для примера выше оптимальным будет такое дерево:
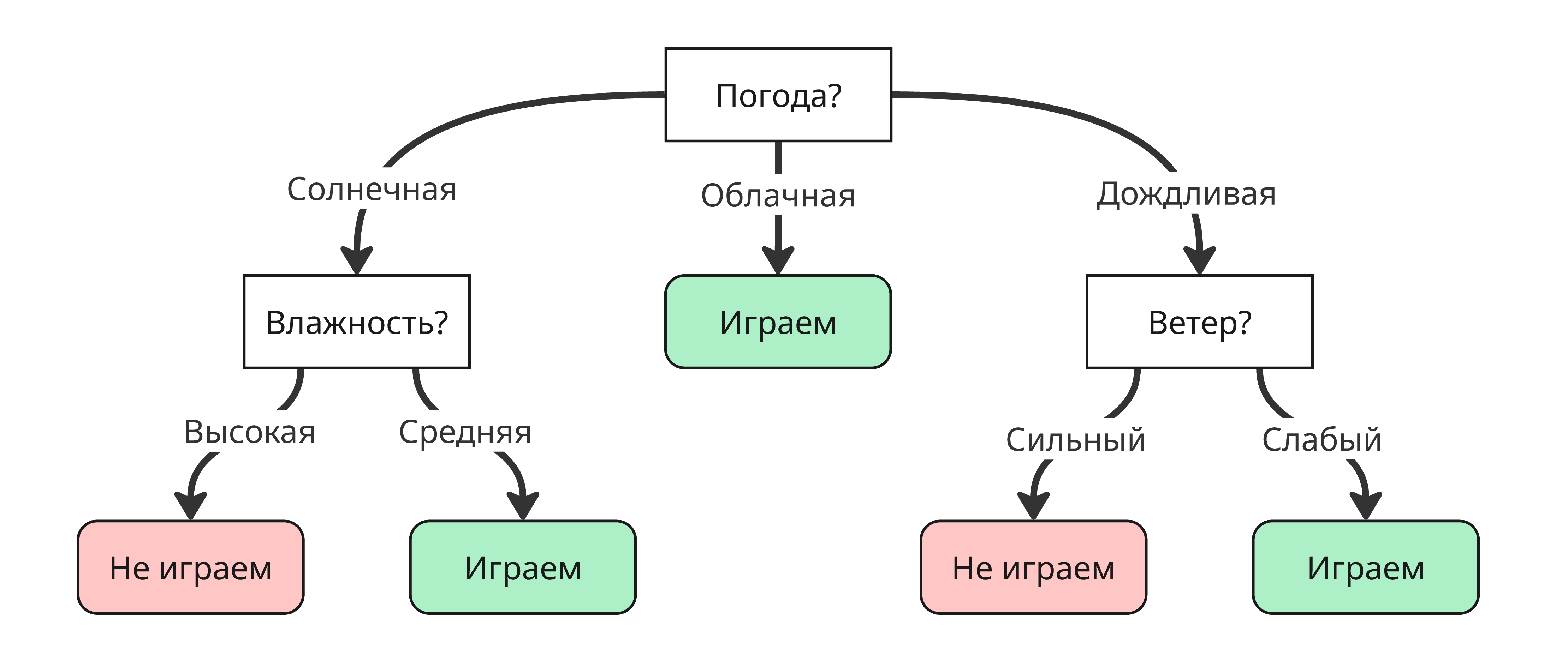
Из этого возникает вопрос: как его построить оптимальный способом?
Это определяется с помощью величины энтропии для каждого признака. Энтропия показывает меру неопределенности эксперимента и считается так:
\[H(S) = - \sum_{k = 1}^d p_k \log_2 p_k,\]где $d$ - число классов, $p_k$ - доля класса $k$ в выборке $S$
Тогда для всей нашей выборки $H(S) = - \frac{9}{14} \log_2 \frac{9}{14} - \frac{5}{14} \log_2 \frac{5}{14} \approx 0.94$
Далее для каждой подвыборке, которой соответствует значение какого-либо признака считается энтропия:
| Признак | Значение | Энтропия |
|---|---|---|
| Погода | Солнечная | $-\frac{2}{5} \log_2 \frac{2}{5} - \frac{3}{5} \log_2 \frac{3}{5} \approx 0.97$ |
| Облачная | $-\frac{4}{4} \log_2 \frac{4}{4} - \frac{0}{4} \log_2 \frac{0}{4} = 0$ | |
| Дождливая | $-\frac{2}{5} \log_2 \frac{2}{5} - \frac{3}{5} \log_2 \frac{3}{5} \approx 0.97$ | |
| Температура | Тепло | $-\frac{2}{6} \log_2 \frac{2}{6} - \frac{4}{6} \log_2 \frac{4}{6} \approx 0.92$ |
| Жарко | $-\frac{2}{4} \log_2 \frac{2}{4} - \frac{2}{4} \log_2 \frac{2}{4} = 1$ | |
| Холодно | $-\frac{3}{4} \log_2 \frac{3}{4} - \frac{1}{4} \log_2 \frac{1}{4} \approx 0.81$ | |
| Влажность | Высокая | $-\frac{3}{7} \log_2 \frac{3}{7} - \frac{4}{7} \log_2 \frac{4}{7} \approx 0.98$ |
| Средняя | $-\frac{6}{7} \log_2 \frac{6}{7} - \frac{1}{7} \log_2 \frac{1}{7} \approx 0.59$ | |
| Ветер | Слабый | $-\frac{3}{6} \log_2 \frac{3}{6} - \frac{3}{6} \log_2 \frac{3}{6} = 1$ |
| Сильный | $-\frac{6}{8} \log_2 \frac{6}{8} - \frac{2}{8} \log_2 \frac{2}{8} \approx 0.81$ |
Далее для каждого признака считается информационный выигрыш (IG, Informational Gain) по формуле:
\[\mathrm{IG}(S, A) = H(S) - \sum_{v \in A} \frac{\vert S_v \vert}{\vert S \vert} H(S_v),\]где $S_v$ - подвыборка, где у всех элементов значение $v$ признака $A$
Получаем следующие значения:
| Признак | Информационный выигрыш |
|---|---|
| Погода | 0.247 |
| Влажность | 0.152 |
| Ветер | 0.048 |
| Температура | 0.029 |
Информационный выигрыш показывает, насколько важен признак в выборке и насколько сильно он снизит энтропию при разделении
Как можно заметить, “Погода” имеет наиболее сильный информационный выигрыш, поэтому первая вершина в дереве будет разделять дерево по “Погоде”
Вместо энтропии также можно использовать вычислительно простой индекс Джини (Gini): $\mathrm{Gini}(S) = 1 - \sum_{k = 1}^d p_k^2$. В таком случае самый важный признак выбирают таким образом, чтобы индекс Джини уменьшался, то есть максимизируют $\Delta \mathrm{Gini}(S, A) = \mathrm{Gini}(S) - \sum_{v \in A} \frac{\vert S_v \vert}{\vert S \vert} \mathrm{Gini}(S_v)$
Для дискретных признаков достаточно перебрать всех значения для подсчета информационного выигрыша. Если их очень много или признак непрерывный, то можно перебирать по интервалам
Останавливать разбиение можно, используя несколько критериев:
- Когда остался только один класс
- Когда один из классов в подвыборке пуст после разбиения, из-за чего появляется сильный дисбаланс
- Когда прирост критерия $\Phi(S)$ (например, энтропия или индекс Джини) становится меньше заданного порога - дальнейшие разбиения не улучшают модель значительно, и, наоборот, могут привести к переобучению
- Размер подвыборки меньше конкретного порога - мало примеров, нельзя сделать статистические выводы
- Высота дерева выше конкретного порога - если она слишком большая, то начинается переобучение
- Через статистические тесты - если нет статистически значимой связи
Если после остановки в выборке осталось несколько классов, то выбираем наиболее вероятный
Деревья решения можно использовать в регрессии - получатся регрессионные деревья. В листе вместо класса возвращается среднее значение:
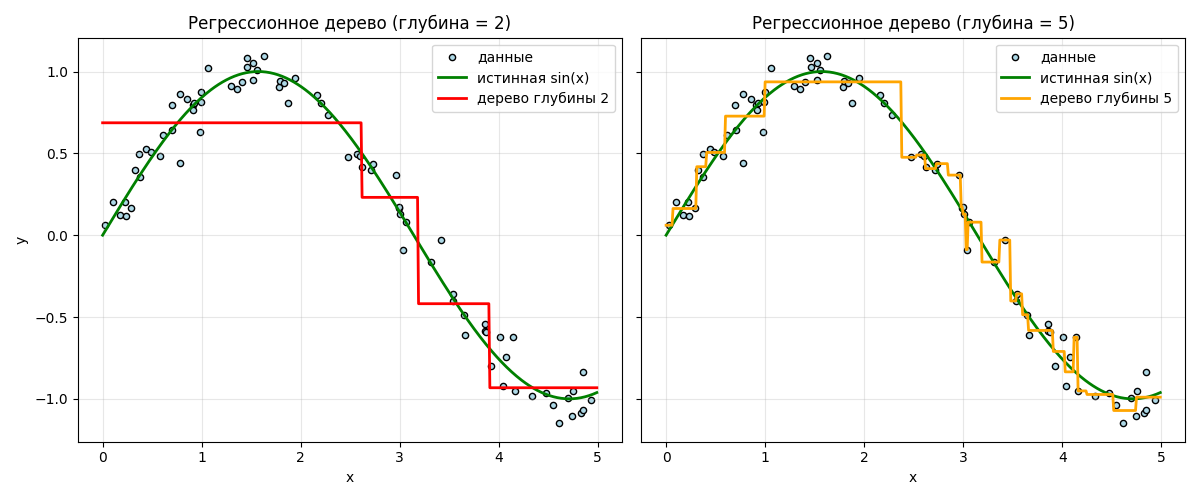
Здесь хорошо видно, что дерево с высотой 5 имеет небольшое переобучение. Структура деревьев выглядит так:
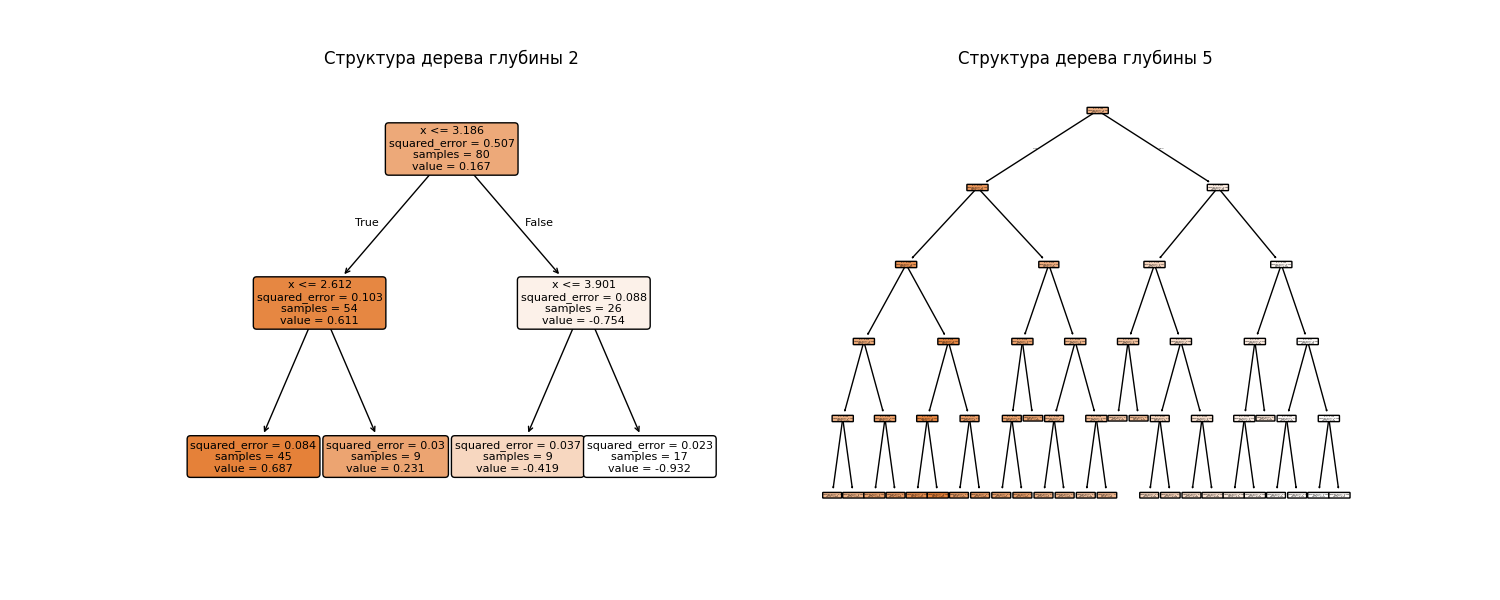
Код примера: machlearn_regression_tree.py
Для регрессионных деревьев можно использовать дисперсию подвыборки как критерий остановки
Проблема в глубоких деревьях - переобучение. Однако невысокие деревья не смогут показать хорошие результаты при больших признаках. Поэтому появилась теорема Шапире, сформулированная в 1990 году (ссылка на статью - *тык*):
Слабая обучаемость эквивалентна сильной обучаемости
Здесь
- слабая обучаемость означает, что алгоритм способен находить гипотезу, которая чуть-чуть лучше случайного угадывания
- сильная обучаемость - алгоритм способен достичь сколь угодно малой ошибки, если дать ему достаточно данных
Если мы можем создать алгоритм, который обучается хоть немного лучше случайного, то, повторяя и комбинируя его результаты, мы можем построить сильный классификатор
Поэтому можно сделать кучу слабо обученных деревьев (то есть с малой глубиной), которые ошибаются в соответственно разных местах, но которые в композиции дают хороший результат
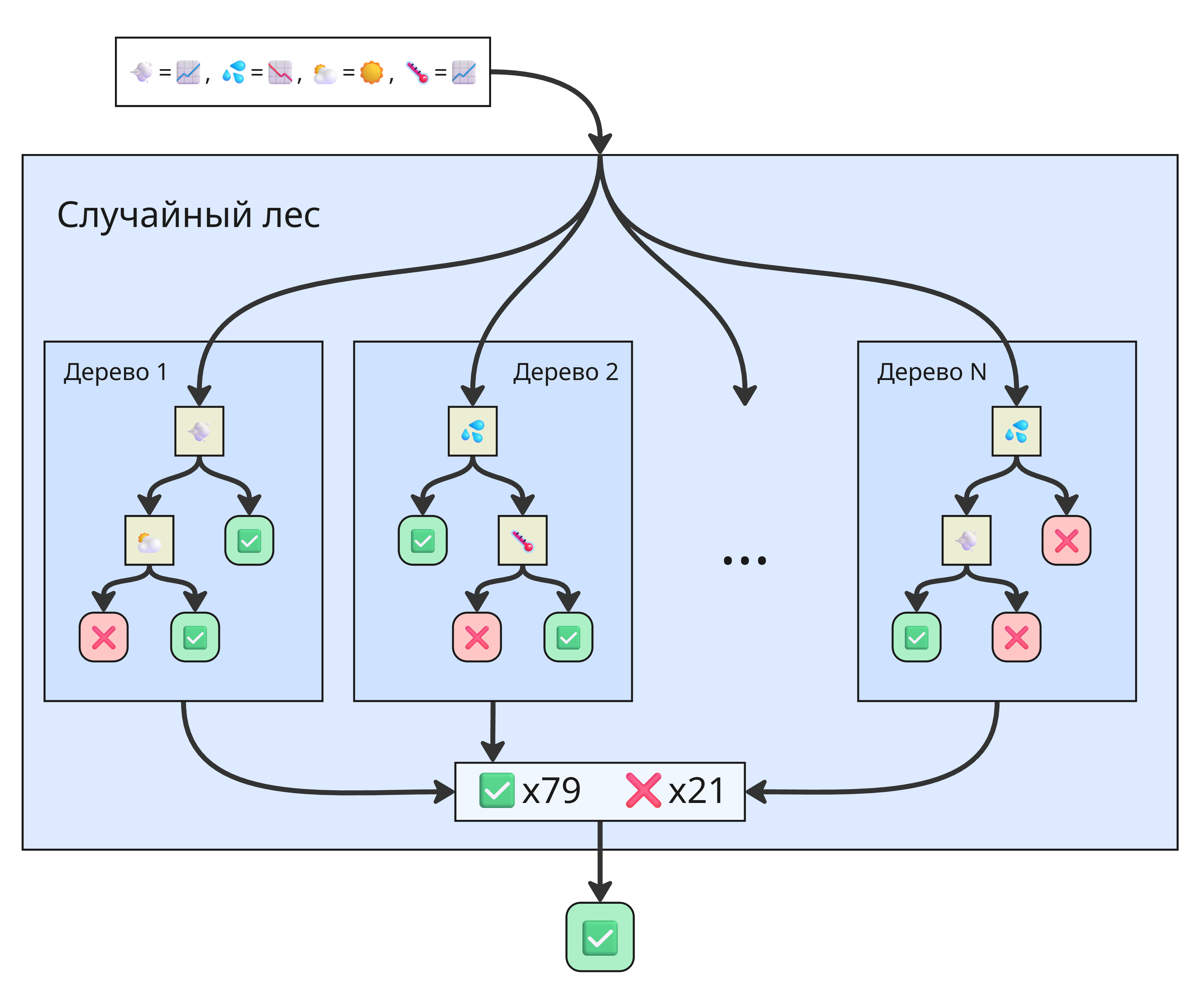
Такой подход называется лесом деревьев решений. Работает лес так:
-
Бутстрэппинг (или бэггинг, от bootstrap aggregating) данных
Из исходной обучающей выборки случайно выбираются подвыборки. Каждое дерево обучается на своей подвыборке
-
Случайный выбор признаков
При каждом разбиении узла дерево рассматривает не все признаки, а только случайно выбранное подмножество. Это снижает корреляцию между деревьями и делает ансамбль более устойчивым
-
Обучение множества деревьев
Строится, например, 100 или 500 деревьев, причем каждое независимо
-
Агрегация результатов:
В классификации могут браться большинство голосов деревьев (мажоритарное голосование) или среднее арифметическое вероятностей принадлежности к классу, данных от каждого дерева (мягкое голосование)
В регрессии берётся среднее значение предсказаний деревьев
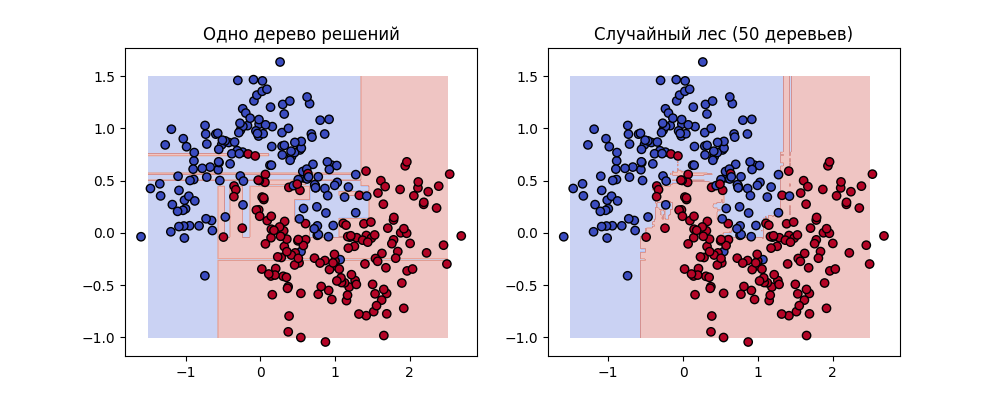
Получаем случайный лес - ансамблевый метод, представляющий собой коллекцию независимых деревьев решений. Пример различий:
Помимо леса можно применить другой подход - бустинг. В бустинге первое дерево обучается на тренировочном датасета и в ходе теста выдаст нам какое-то число неправильных результатов. Далее мы используем веса, чтобы сделать веса больше примерам из выборки, предсказания для которых были ошибочными, и на них тренируем второе дерево и так далее. Такой процесс повторяется много раз, и итоговая модель представляет собой взвешенную композицию всех деревьев, где каждое дерево уточняет предсказания предыдущих
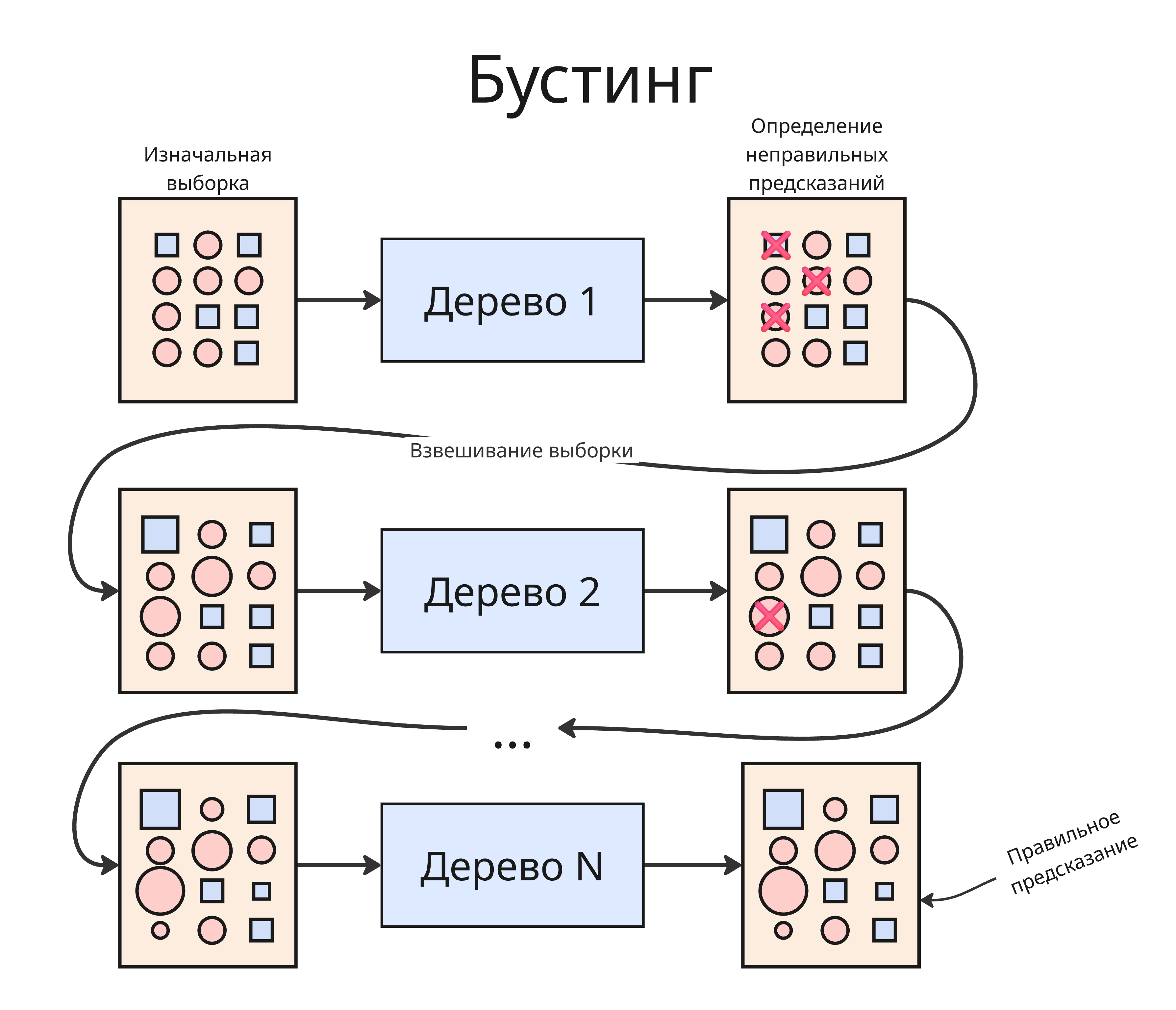
Веса можно уточнять с помощью градиентного спуска. Рассмотрим 3 реализации градиентного бустинга:
-
LightGBM (Light Gradient Boosting Machine)
- Производит разделение в вершине, где прирост критерия наибольший. Это даёт высокую точность, но может привести к переобучению
- Применяет градиентную выборку (GOSS) - использует не все объекты, а только те, где ошибка большая
- Отлично работает с большими табличными данными
Обычно LightGBM - самый быстрый из трёх, особенно на больших датасетах
-
XGBoost (Extreme Gradient Boosting)
- Строит деревья последовательно по достижению максимальной глубины
- Поддерживает регуляризацию (L1 и L2), то есть меньше переобучается
- Оптимизирован для параллельной работы и кэширования
Считается “золотым стандартом” бустинга: баланс между точностью и устойчивостью.
-
CatBoost (Categorical Boosting)
- Строит деревья, в которой один уровень вершин - это разделение по одному признаку
- Не требует кодировки категорий и умеет работать с категориальными данными напрямую
- Использует упорядоченный бустинг - при обучении каждой модели данные переставляются
- Имеет понятную визуализацию важности признаков
Очень устойчив к переобучению
Также есть еще один ансамблевый подход - стекинг. В стекинге (stacking)
- Сначала обучаются модели одного типа на исходном датасете
- На новой выборке получаем предсказания
- Другая модель на этом наборе предсказаний обучается