itmo_conspects

Лекция 7. Метод опорных векторов

Метод опорных векторов (Support Vector Machine, SVM) - это алгоритм классификации, который ищет гиперплоскость, разделяющую данные разных классов с максимальным зазором (margin)

Пусть дана выборка из переменных $X$ и класс для каждой точки $y_i \in {-1, 1}$

Гиперплоскость мы будем искать в виде $w^T x + b = 0$, где $w$ - вектор весов, $x$ - точка в пространстве

Ближайшие к этой гиперплоскости точки из нашей выборки называют опорными векторами. Плоскость должна быть такой, что бы расстояние от нее до опорных векторов было максимальным

Так как гиперплоскость разделяет точки по их классам, то выполняется условие $y_i (w^T x_i + b) \geq 1$. Для опорных векторов $y_i (w^T x_i + b) = 1$

Несложно показать, что ширина зазора равна $\frac{2}{| w |}$ ($\frac{2}{| w |} = \frac{\vert w^T x + b + 1 \vert - \vert w^T x + b - 1 \vert}{|w|}$ - расстояние между точками, удаленных на один от точки $x$ на гиперплоскости)

Тогда, чтобы увеличить ширину, нужно уменьшить $| w |$, то есть метод опорных векторов решает задачу:

\[\frac{1}{2} \|w\|^2 \longrightarrow \min \text{ при условии, что } y_i (w^T x_i + b) \geq 1\]

Такой подход называется методом опорных векторов с жестким зазором (Hard-margin SVM)

Здесь мы минимизируем $|w|^2$, так как $| w | = \sqrt{w_1^2 + \dots + w_n^2}$ не дифференцируема в $\vec 0$

Веса ищутся с помощью градиентного спуска

---

Рассмотрим случай для двухмерных точек. Допустим, что они линейно разделимые, то есть гиперплоскость (в нашем случае линия) разделяет их. Тогда получаем такую картину:

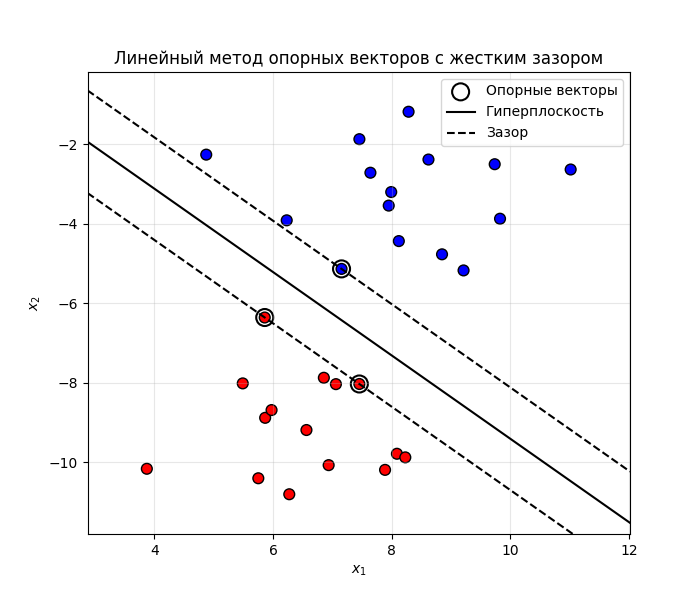
Код примера - machlearn_svm_hard_margin.py

Если данные линейно не разделимы, то есть их нельзя разделить плоскостью, то можно применить два трюка:

1. Метод опорных векторов с мягким зазором (Soft-margin SVM)

   Добавляем штраф $\xi_i$ для каждой точки:

   • Если точка на границе зазора или за пределами, то она классифицирована правильно, и для нее $\xi_i = 0$
   • Если точка внутри зазора, но на правильной стороне от гиперплоскости, то она классифицирована правильно, и для нее $0 < \xi_i \leq 1$
   • Если точка по другую сторону от гиперплоскости и классифицирована неправильно, то для нее $\xi_i > 1$

   Тогда условие становится таким: $y_i (w^T x_i + b) \geq 1 - \xi_i$

   Теперь будем минимизировать такое выражение:

   \[\frac{1}{2} \|w\|^2 + C \sum_{i = 1}^n \xi_i \longrightarrow \min \text{ при условии, что } y_i (w^T x_i + b) \geq 1 - \xi_i\]

   Здесь $C$ - гиперпараметр, управляющий штрафом за ошибки. При большом $C$ модель пытается строго разделить данные, а при меньшем $C$ модель допускает больше ошибок

   

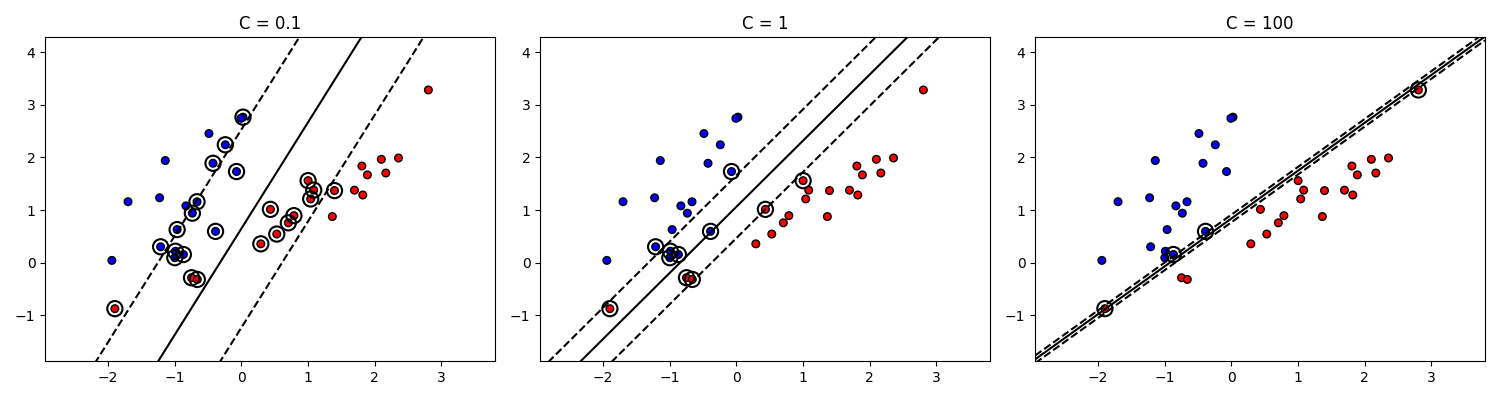
   Код примера - machlearn_svm_soft_margin.py

   Очевидно, что при большом $C$ также уменьшается ширина зазора. В пределе $C \to \infty$ метод опорных векторов с мягким зазором превращается в метод опорных векторов с жестким зазором

2. Нелинейный метод опорных векторов

   Если данные вообще жесть как не разделимы, то можно прибегнуть

   • К увеличению размерности пространства, например, представить двухмерные точки $(x_1, x_2)$ как $(x_1^2, x_2^2, \sqrt{2} x_1 x_2)$ и искать гиперплоскость в трехмерном пространстве:

     

     Код примера - machlearn_svm_dimension_increase.py

     Зачастую размерность исходного пространства большая, увеличение размерности повышает его экспоненциально, поэтому применяют следующий трюк

   • Или к переопределению скалярного произведения через ядерные функции

     Вместо линейного скалярного произведения $K(x, y) = (x, y) = \sum_{i = 1}^n x_i y_i$ (так называемое линейное ядро, linear kernel) можно взять:

     • Полиномиальное ядро (Polynomial kernel): $K(x, y) = (\gamma (x, y) + r)^d$, где $\gamma$ - масштаб, $r$ - смещение, $d$ - степень полинома

     • Гауссовское ядро (или RBF, Radial Basis Function): $K(x, y) = e^{-\gamma |x - y|^2}$, где $\gamma$ - регулирует масштаб функции. При маленьких $\gamma$ граница гладкая (функция сходится к 0 медленнее), а при больших $\gamma$ - более изогнутая. Самое такое мейнстримное ядро

     • Сигмоидное ядро (Sigmoid kernel): $K(x, y) = \mathrm{tanh}(\gamma (x, y) + r)$

     Тогда мы не вычисляем новые признаки явно, а сразу считаем скалярное произведение в этом новом пространстве, то есть экономим время и память (так называемый Kernel Trick)

Подходы можно комбинировать, получится нелинейный метод опорных векторов с мягким зазором:

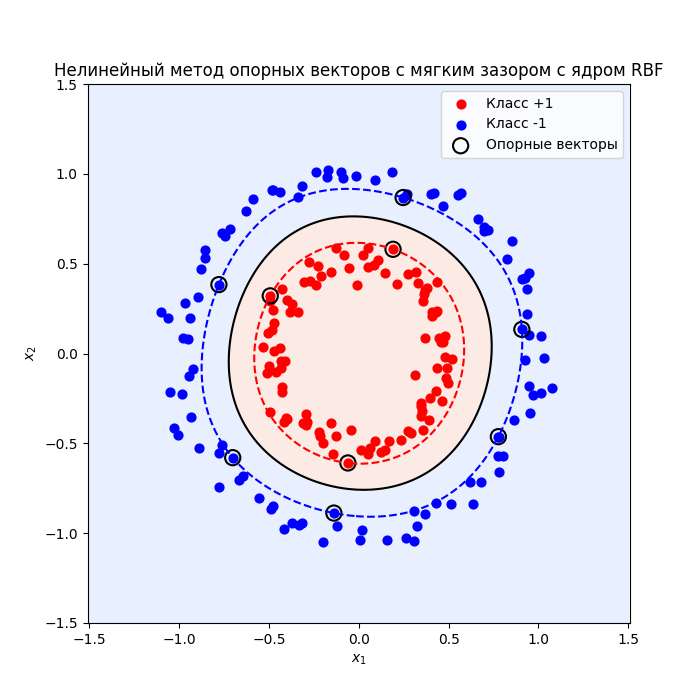
Еще пример:

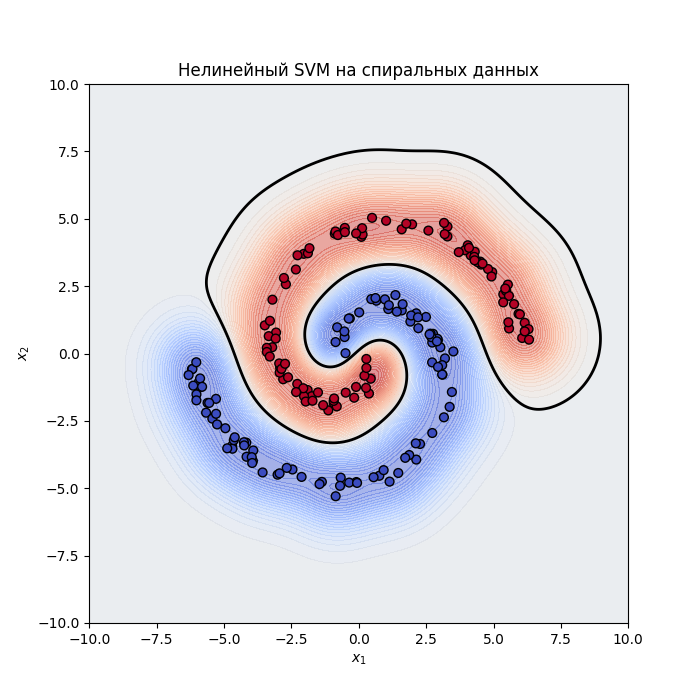
Код примера - machlearn_svm_nonlinear.py, machlearn_svm_nonlinear_2.py

This site is open source. Improve this page.