itmo_conspects
Лекция 6. Линейная регрессия
Регрессия - односторонняя зависимость, устанавливающая соответствие между случайными величинами. Регрессию не стоит путать с классификацией, потому что, хотя обе задачи относятся к предсказательному моделированию, их цели и тип выходных данных принципиально различаются.
В регрессии модель пытается предсказать непрерывное числовое значение, а в классификации модель решает задачу отнесения объекта к одному из заранее известных классов
Рассмотрим линейную регрессию, которая предполагает, что зависимость между данными линейная. Модель линейной регрессии формулируется так:
\[a(x) = \sum_i w_i x_i = (\vec w, \vec x),\]где $a(x)$ - предсказанный результат, $\vec w$ - вектор весов, а $\vec x$ - вектор факторов, для которых предсказывается результат
Чтобы регрессия насколько можно хорошо предсказывала результат, нужно уменьшиться количество ошибок - для этого вводят функцию потерь $L(w)$. Значения весов находятся в результате минимизации функции потерь. За функцию потерь можно взять:
-
Дисперсия ошибок $\mathrm{MSE}(w) = \frac{1}{n} \sum_{i = 1}^n (\vec x^{(i)} \cdot \vec w - y_i)^2$ - тогда получается метод наименьших квадратов
$\mathrm{MSE}(w)$ возводит в квадрат значения, поэтому штрафует за выбросы и большие ошибки, однако квадрат размерности плохо интерпретируется
- Среднее значение абсолютных разностей $\mathrm{MAE}(w) = \frac{1}{n} \sum_{i = 1}^{n} \vert x^{(i)} \cdot \vec w - y_i \vert$
- Среднее квадратическое отклонение $\mathrm{RMSE}(w) = \sqrt{\mathrm{MSE}(x)}$
Чтобы найти минимум функции, продифференцируем ее, но продифференцировать нужно по всем компонентам $w$, то есть взять градиент:
\[\nabla L(w) = \begin{pmatrix}\frac{\partial L}{\partial w_0} \\ \frac{\partial L}{\partial w_1} \\ \vdots \\ \frac{\partial L}{\partial w_d} \end{pmatrix}\]Для метода наименьших квадратов это превращается в такую систему линейных алгебраических уравнений: $\nabla L(\hat w) = 2 \sum_{i = 1}^n \vec x_i (\vec x_i \cdot \hat w - y_i) = 0$, где ищем вектор $\hat w$
Или $\hat w \sum_{i = 1}^n \vert \vec x_i \vert^2 = \sum_{i = 1}^n \vec x_i y_i$
В матричной форме это $\hat w = (X^T X)^{-1} X^T Y$
Такой подход, аналитический, дает оптимальное решение, однако очень медленно вычисляется (инверсия матрицы занимает $O(n \cdot d^2 + d^3)$), а если матрица $X$ линейно зависима (то есть в выборке две одинаковых строки или один признак линейно зависит от других), то определитель будет равен 0, что делает невозможным вычисление обратной матрицы
Градиент указывает на направление наибольшего роста, тогда в противоположном направлении будет находится локальный минимум функции
В итоге численный метод вычисления локального минимума вектора $w$ будет выглядеть так:
\[w^{(k + 1)} = w^{(k)} - \alpha_{k} \Delta L(w^{(k)})\]где $w^{(k)}$ - веса на текущей итерации, $w^{(k + 1)}$ - веса на следующей итерации, $\alpha_{k}$ - коэффициент, определяющий скорость сходимости (так называемый learning rate)
Скорость спуска $\alpha_{k}$ подбирается эмпирически, и его эффективность зависит от характера функции потерь. Например, в простейшем случае для вектора $w$ из одного элемента и функции $L(w)$ при разных $\alpha_{k}$ можем получить такую картину:
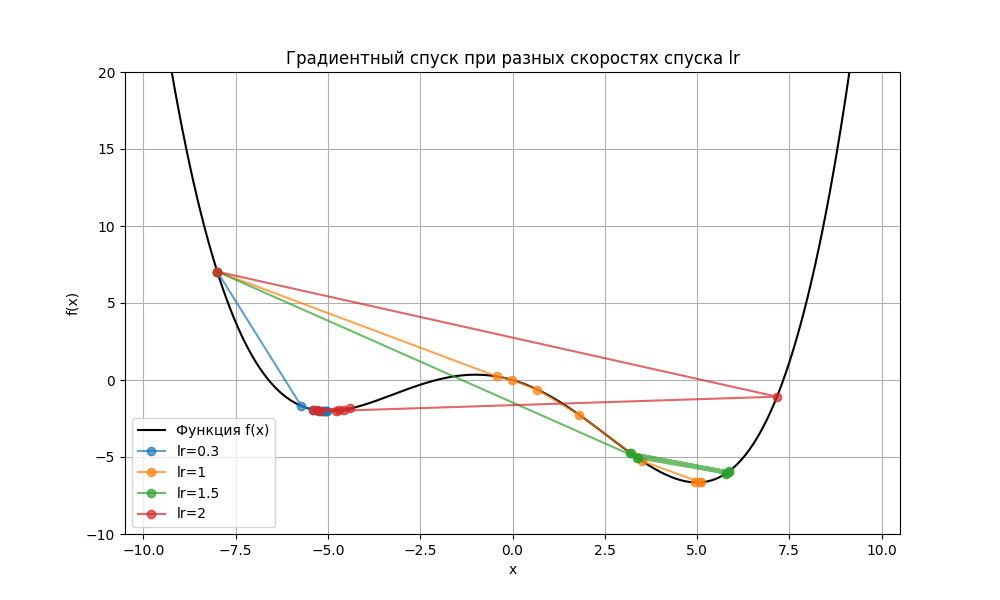
Здесь при lr = 0.3 (синяя ломаная) алгоритм нашел локальный минимум функции в точке -5, но не глобальный. Также и при lr = 2 (красная ломаная) алгоритм перепрыгнул глобальный минимум. При lr = 1 (желтая ломаная) минимум был найден, но при lr = 1.5 (зеленая ломаная) алгоритму было недостаточно 8 итераций, чтобы его найти
Из-за этого скорость спуска делает непостоянной, например, убывающей:
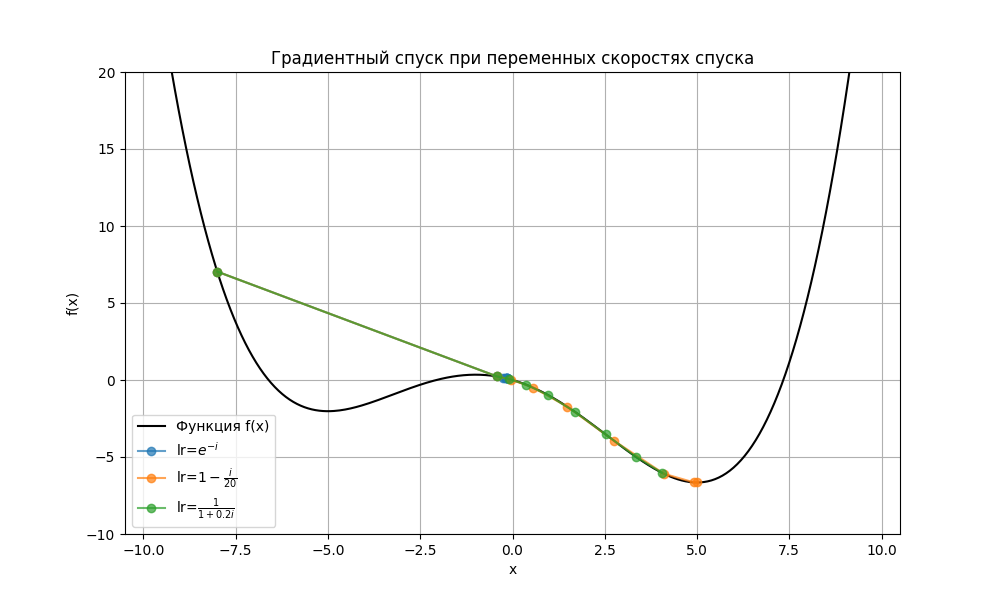
Код примера - machlearn_gradient_descent.py
Помимо скорости спуска, сходимость градиентного спуска также зависит от:
- топологии функции, например, в седловой точке, на плато или в местах смены выпуклости производные по некоторым переменным равны 0
- типа функции потерь
- шума в градиенте при использовании стохастического или пакетного спусков (о них позже)
- методов оптимизации
- начальной точки
Также использование всей выборки (а ее размер может быть порядка тысяч) может замедлять вычисления (такой подход называется полный градиентный спуском). Поэтому можно:
-
Вычислять градиент для одного случайного элемента из выборки - стохастический градиентный спуск (Stochastic Gradient Descent):
\[w^{(k + 1)} = w^{(k)} - \alpha_{k} \nabla Q(w^{(k)}),\]где $Q(w^{(k)})$ - функция потерь для одного случайного элемента
Стохастическому градиентному спуску требуется больше итераций, но итерация длится меньше
Чтобы ускорить сходимость, можно воспользоваться стохастическим градиентным спуском с инерцией:
\[w^{(k + 1)} = w^{(k)} - \alpha_{k} \nabla Q(w^{(k)}) + \mu \Delta w^{(k)},\]где $\Delta w^{(k + 1)} = \Delta w^{(k)} - \alpha_{k} \nabla Q(w^{(k)})$
-
Вычислять градиент для нескольких случайных элементов из выборки - пакетный градиентный спуск (Mini-batch Gradient Descent)
\[w^{(k + 1)} = w^{(k)} - \alpha_{k} \nabla L_B (w^{(k)}),\]где $L_B(w^{(k)})$ - функция потерь для подвыборки размером $B$
Сходимость пакетного спуска зависит от размера пакета, набора элементов из выборки. Чем больше пакет, тем меньше шумов и длиннее итерация

Также начальная точка спуска может выбираться случайно, чтобы наиболее вероятно найти глобальный минимум
Ключевой метрикой линейной регрессии является $R^2 = 1 - \frac{\sum (y_i - \hat y_i)^2}{\sum (y_i - \overline{y})^2}$ - коэффициент детерминации, показывающий, какую долю дисперсии предсказываемого признака способна модель объяснить
На основе его вводят другую метрику $R^2_{\text{adj}} = 1 - \left(\frac{(1 - R^2) (n - 1)}{n - p - 1}\right)$ - скорректированный коэффициент детерминации, где $n$ - размер выборки, $p$ - число независимых признаков. Такая метрика сильно понижается, если параметров слишком много, тем самым, предотвращая переобучение
Чтобы сделать модель проще, введем штраф за число весов. Есть несколько подходов:
-
Лассо (L1-регуляризация) добавляет штраф за сумму модулей весов:
\[L_1 (w) = L(w) + \lambda \sum_i \vert w_i \vert\]Подходит для разреженных данных, но не устойчив к коррелированным признакам
-
Ридж-регрессия (Ridge Regression, L2-регуляризация или регуляризация Тихонова) добавляет штраф за квадрат нормы вектора весов:
\[L_2 (w) = L(w) + \lambda \sum_i w_i^2\]Наказывает большие веса, хорошо работает при коррелированных признаках
-
Эластичная сеть (Elastic net regularization) является комбинацией предыдущий двух регуляризаций:
\[L_{1,2} (w) = L(w)+ \lambda_1 \sum_i \vert w_i \vert + \lambda_2 \sum_i w_i^2\]Почти всегда устойчив к коррелированным признакам, подходит для разреженных данных. Эластичную сеть следует использовать, когда количество признаков больше количества объектов
Также с помощью регрессии можно решить задачу классификации. Пусть положительное $y_i$ означает, что точка $x_i$ принадлежит классу 1, а отрицательное - классу -1. Тогда $\hat y = \mathrm{sign}((\vec w, \vec x))$
Помимо этого мы хотим быть уверены в предсказании, поэтому нужна функция, которая для $(\vec w, \vec x) \in \mathbb{R}$ даст вероятность принадлежности из отрезка $[0, 1]$. В качестве нее можно взять сигмоиду: $f(\vec w, \vec x) = \frac{1}{1 + e^{-(\vec w, \vec x)}}$
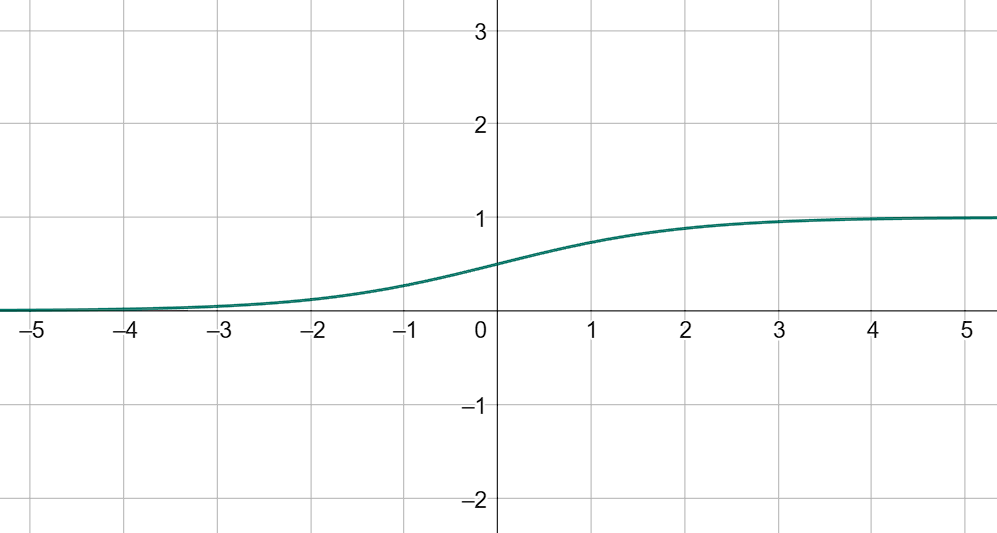
Отсюда $(\vec w, \vec x) = \ln \left(\frac{p}{1 - p}\right)$
Тогда функция потерь формулируется так: $L(w) = \sum_{i = 1}^n \left(y_i \ln(p) + (1 - y_i) \ln(1 - p)\right)$
Такой подход решения классификации с помощью регрессии называется логистической регрессией