itmo_conspects
Лекция 5. Метрики, метод k ближайших соседей
Во время обучения модели возникает компромисс отклонение-дисперсия (Bias-variance tradeoff): ошибку модели, то есть то, насколько ее предсказывание неверно от реального результата, можно поделить на три части:
- Смещение - погрешность оценки, возникающая в результате ошибочного предположения в алгоритме обучения
- Дисперсия - ошибка чувствительности к малым отклонениям в тренировочном наборе
- Шум - дополнительная ошибка, которую никак нельзя предсказать
Более простые, недообученные модели склонны иметь большое смещение, а более сложные, переобученные очень чувствительные к значениям переменных и не способны предсказывать общую закономерность
Поэтому данные делят на три части:
- Тренировочные данные (Train set) - это данные, на которых модель обучается, то есть подбирает свои параметры
- Тестовые данные (Test set) - это данные, на которых оценивается качество модели, которые модель не видела во время обучения
-
Данные для проверки (Validation set) - для более точного подбора гиперпараметров модели путем их проверки на этих данных
Гиперпараметры же находятся с помощью данных для проверки:
- подбором
- рандомом
- техниками оптимизации
Главная цель - проверить, насколько модель обобщается на новые, невиданные данные. Это нужно, чтобы:
-
Предотвратить переобучение - ситуацию, когда модель слишком хорошо запомнила тренировочные данные, но при этом плохо обобщает на новые данные (тестовые или реальные)
-
Если проверять модель на тех же данных, на которых она обучалась, результат будет чрезмерно оптимистичным
-
Модель может запомнить конкретные примеры, но не научится общим закономерностям
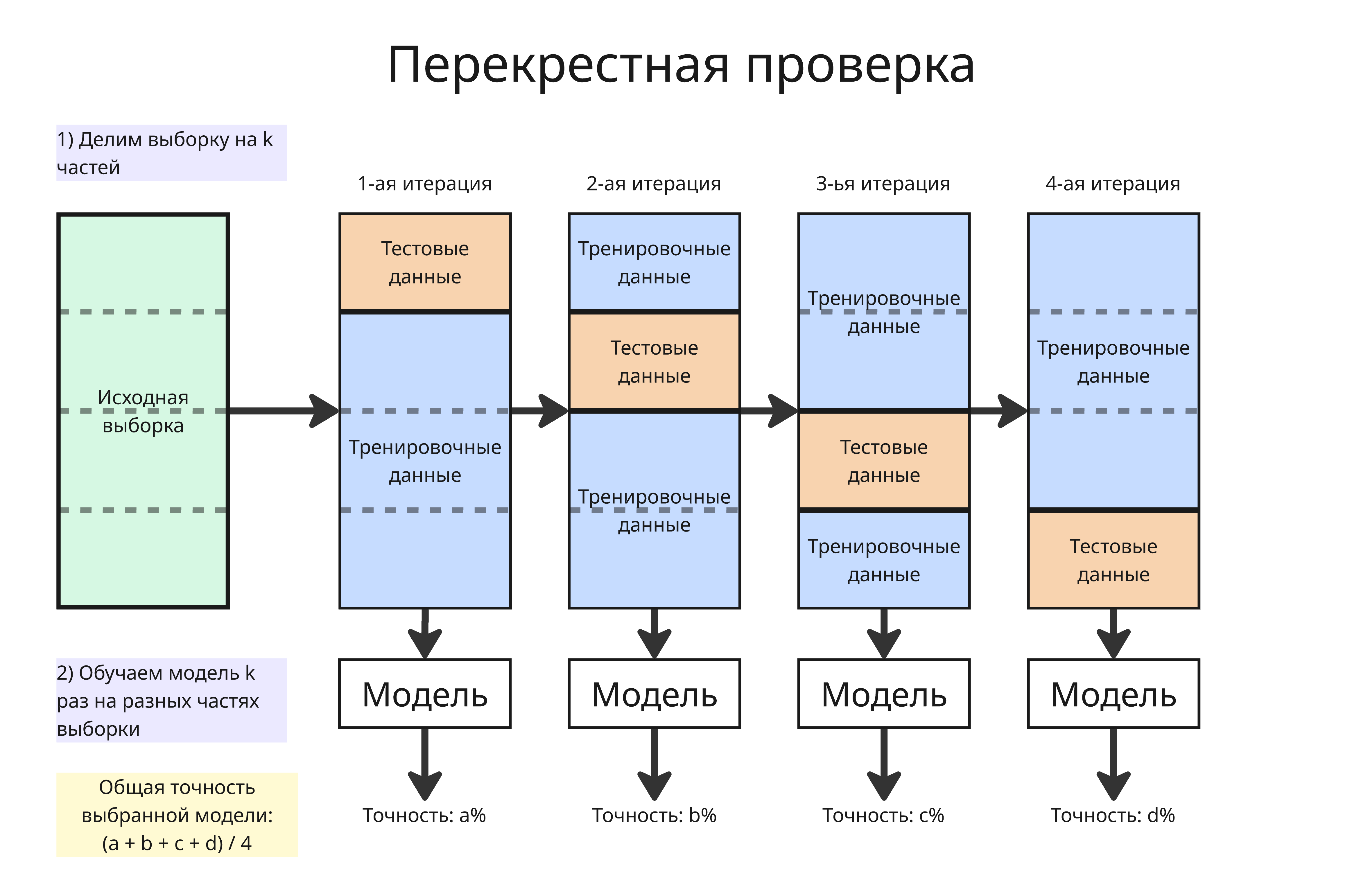
В том числе для предотвращения переобучения используется перекрестная проверка (K-Fold Cross Validation):
- Выборка делится на
kчастей - Далее каждая из частей становится тестовыми данными, а остальные - тренировочными
- Модель обучается на тренировочных, проверяется на тестовых, получаем
kопределенных метрик дляkобученных моделей - Берется общее этих метрик (например, среднее арифметическое), чтобы оценить точность и эффективность с наиболее равномерным использованием имеющихся данных
Зачастую датасеты могут быть несбалансированными, то есть намного чаще обладать одним признаком А, нежели другим признаком B (например, список транзакций, где чаще всего будут успешные), что помешает обучению модели. Для решения этого есть такие методы:
-
Добавление примеров меньшего класса (Oversampling)
Добавление примеров может привести к переобучению, если просто дублировать данные
Самый известный метод добавления - SMOTE (о нем позже)
-
Уменьшение примеров большего класса (Undersampling)
При уменьшении мы случайно удаляем часть примеров из преобладающего класса. При этом мы теряет часть информации из обучающего набора
-
Взвешивание классов: увеличиваем вес редкому классу в функции потерь
-
Изменение порога классификации
Метрики
Методы машинного обучения в основном решают две задачи:
- Классификация - предсказание принадлежности объекта к классу
- Регрессия - предсказание результата на основе неявной закономерности или корреляции
Чтобы понять, насколько хороша наша модель классификации, допустим, что наша модель выводит 0 или 1 в качестве результата, посчитаем, столько таких результатов:
- Истинно положительные (True Positive, TP) - такие, в которых модель права и выдала 1
- Истинно отрицательные (True Negative, TN) - такие, в которых модель права и выдала 0
- Ложноположительные (False Positive, FP) - такие, в которых модель ошиблась и выдала 1
- Ложноотрицательные (False Negative, FN) - такие, в которых модель ошиблась и выдала 0
Тогда составим следующие метрики:
-
Аккуратностью (Accuracy) модели называют долю верно предсказанных результатов от всех: $\displaystyle \mathrm{Accuracy} = \frac{\mathrm{TP} + \mathrm{TN}}{\mathrm{TP} + \mathrm{TN} + \mathrm{FP} + \mathrm{FN}}$
Аккуратность не работает, если классы не сбалансированы в выборке. Например, если в больнице 95 пациентов здоровы, 5 - больны, а модель предсказала, что все здоровы, то аккуратность будет равна 95%, хотя больных мы не нашли
Аккуратность используется, когда все ошибки одинаково важны
-
Точностью (Precision) модели называют долю истинно положительных от всех предсказанных положительных результатов: $\displaystyle \mathrm{Precision} = \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FP}}$
Точность полезна, когда мы хотим уменьшить число ложноположительных срабатываний, например, для фильтра спама
-
Запоминанием (Recall) модели называют долю истинно положительных от всех действительно положительных результатов: $\displaystyle \mathrm{Recall} = \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FN}}$
Запоминание применяют для уменьшения ложноотрицательных результатов, например, в случае выставления медицинского диагноза
-
F-мера (F-score или F1-score) модели называют гармоническое среднее от точности и запоминания: $\displaystyle F_1 = \frac{2}{\frac{1}{\mathrm{Precision}} + \frac{1}{\mathrm{Recall}}} = \frac{2 \mathrm{Precision} \cdot \mathrm{Recall}}{\mathrm{Precision} + \mathrm{Recall}} = \frac{2\mathrm{TP}}{2\mathrm{TP} + \mathrm{FN} + \mathrm{FP}}$
F-мера используется, когда нужен компромисс между точностью и запоминанием. Если одна из метрик низкая, то она сильно занизит F-меру
Зачастую, модель возвращает не 0 или 1, а вероятность того, насколько принадлежит объект к классу. Если вероятность выше установленного порога $\alpha$, то считается, что объект принадлежит классу
-
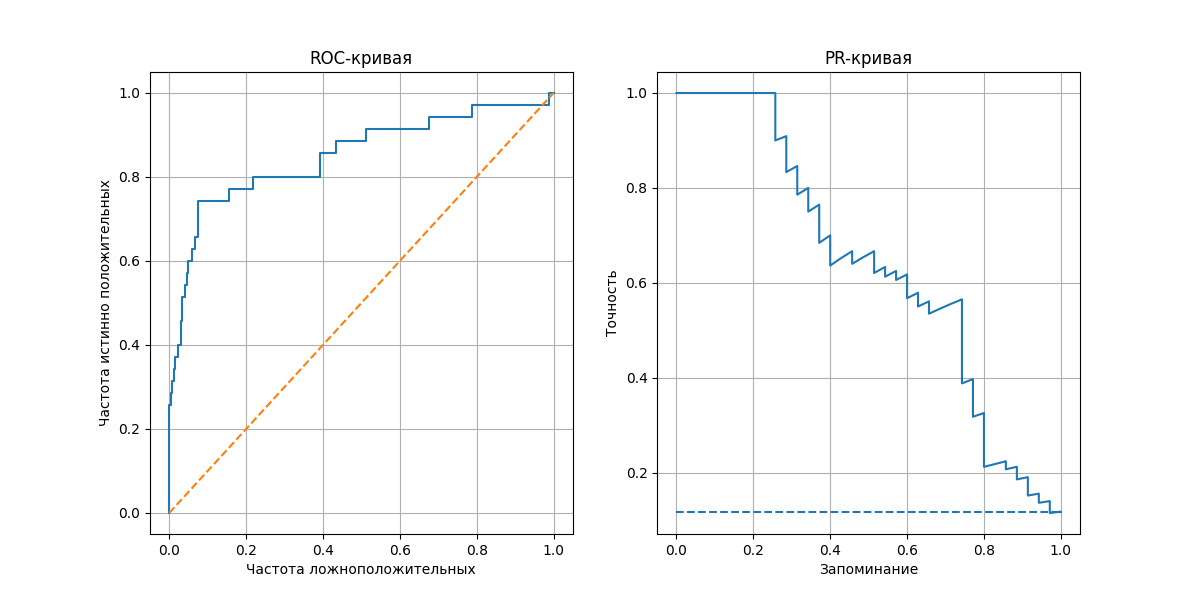
ROC-кривая (Receiver Operating Characteristic) показывает, насколько хорошо модель различает классы. Строится она так:
- Для каждого порога от 0 до 1 считаем, сколько раз мы угадали правильно и неправильно
- Вычисляем две метрики:
- частоту истинно положительных - $\displaystyle \mathrm{True\ Positive\ Rate} = \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FN}}$
- частоту ложноположительных - $\displaystyle \mathrm{False\ Positive\ Rate} = \frac{\mathrm{FP}}{\mathrm{FP} + \mathrm{TN}}$
- Отмечаем точки $(\mathrm{False\ Positive\ Rate}, \mathrm{True\ Positive\ Rate})$ на плоскости, соединяем их - получаем кривую от $(0, 0)$ до $(1, 1)$
Полученная линия показывает, как меняется баланс между количеством ложных срабатываний и истинных попаданий
Площадь под кривой (ROC-AUC, Area Under Curve) - метрика, измеряющая общую способность модели различать классы. Для модели, возвращающей случайные результаты, ROC-кривая представляет прямую из $(0, 0)$ до $(1, 1)$, если полученная кривая располагается выше линии $y = x$ (то есть площадь больше $0.5$), то модель предсказывает лучше, чем случайная модель
-
PR-кривая (Precision-Recall) показывает баланс между точностью и запоминанием при разных порогах классификации. Аналогично, отмечаем точки $(\mathrm{Precision}, \mathrm{Recall})$ для каждого порога
Площадь под кривой PR-AUC высока, если модель находит большинство положительных объектов и делает мало ложных срабатываний. Метрика PR-AUC полезна, если классы в выборке несбалансированны
Если модель решает задачу регрессии, то полезны другие метрики:
-
Среднее значение абсолютных разностей (Mean Average Error) - $\displaystyle \mathrm{MAE} = \frac{1}{n} \sum_{i = 1}^{n} \vert y_i - y_i^\prime \vert$
Метрика устойчива к выбросам
-
Среднее значение квадратов разности (Mean Squared Error) - $\displaystyle \mathrm{MSE} = \frac{1}{n} \sum_{i = 1}^{n} (y_i - y_i^\prime)^2$
Метрика сильно увеличивается, если разность большая
-
Квадратный корень среднего значения квадратов разности (Rooted Mean Squared Error) - $\displaystyle \mathrm{RMSE} = \sqrt{\mathrm{MSE}} = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (y_i - y_i^\prime)^2}$
Метрика в тех же единицах, что и $y_i$
-
Коэффициент детерминации $\displaystyle R^2 = 1 - \frac{\sum (y_i - \hat y_i)^2}{\sum (y_i - \overline{y})^2}$ показывает, какая доля дисперсии $y_i$ объясняется моделью через признаки $x_i$
Если $R^2 = 1$, то модель идеально объясняет все данные. Если $R^2 = 0$, то модель ничего не объясняет, а если $R^2 < 0$ (то есть $\sum (y_i - \hat y_i)^2 > \sum (y_i - \overline{y})^2$), то модель предсказывает хуже, чем модель, которая на каждый запрос выдает среднее $\overline{y_i}$
Метод k ближайших соседей
Метод $k$ ближайших соседей (K-Nearest Neighbors Method) - алгоритм для автоматической классификации объектов
Как он работает:
- Отмечаем точки $x_i$ из нашей выборки на пространстве
- Раскрашиваем их в соответствии с классом (для простоты у нас будут классы 1 и 0)
- Далее отмечаем точку $A$, класс которой мы хотим предсказать
-
Вычисляем расстояния от точки $A$ до точек $x_i$. Это можно делать с помощью:
-
Евклидова расстояния $\displaystyle \mathrm{dist}(x, y) = \sqrt{\sum_{i} (x_i - y_i)^2}$
-
Метрики Манхеттена $\displaystyle \mathrm{dist}(x, y) = \sum_{i} \vert x_i - y_i \vert$ - лучше устойчива к выбросам в пространствах высокой размерности
-
Метрики Минковского $\displaystyle \mathrm{dist}(x, y) = \sqrt[p]{\sum_{i} (x_i - y_i)^p}$
-
Косинусного расстояния $\displaystyle \mathrm{dist}(x, y) = 1 - \frac{x \cdot y}{| x | \cdot | y |}$
-
-
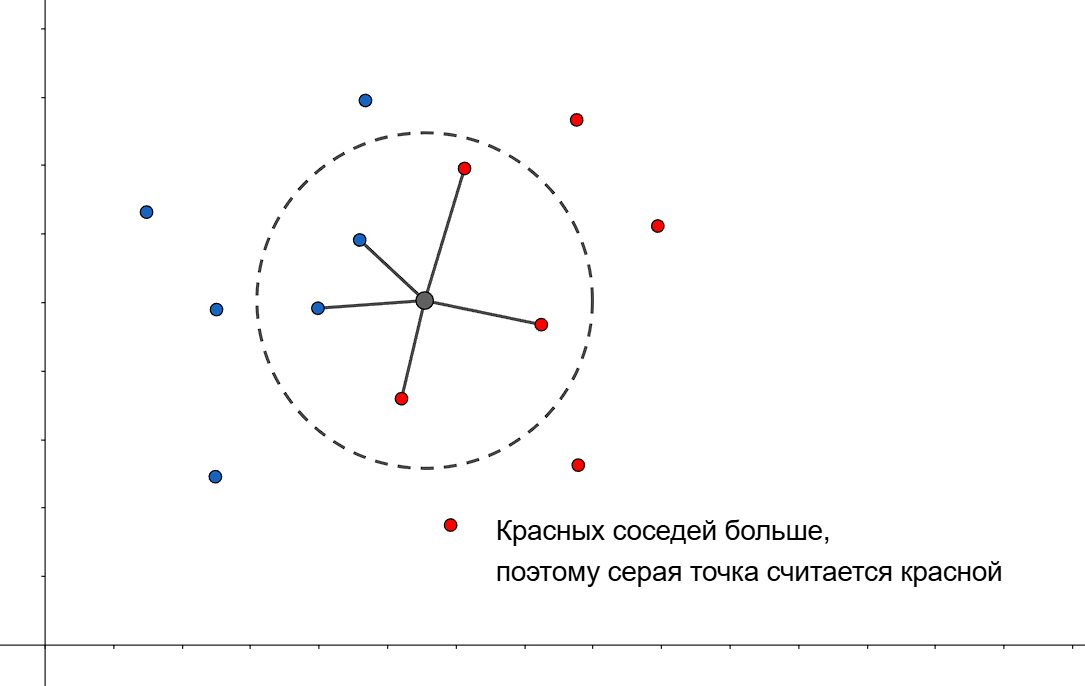
Далее находим $k$ ближайших точек $x_i$ к точке $A$, используя выбранную метрику - назовем их $t_i$
- Пусть $I(t_i, p)$ - индикатор принадлежности к классу $p$. Предсказываем, что точка $A$ принадлежит к классу 1, если среди ее $k$ ближайших соседей больше точек, принадлежащих к 1, чем к 0, то есть $\displaystyle \sum_{i = 1}^k I(t_i, 1) > \sum_{i = 1}^k I(t_i, 0)$
Иногда простой подсчет соседей может не точно предсказывать. Тогда можем применить веса к каждой точке, например $w_i = \frac{k + 1 - i}{k}$ - вес точки линейно уменьшается от порядка в наборе ближайших точек, или $w_i = q^i$, где $q \in (0, 1)$
Однако лучше всего учитывать в весе расстояния до точки. Для этого определим ширину окна $h$ (если расстояние до точки за пределами окна, то считаем ее незначимой) и ядерную функцию $K(x)$
Тогда весом для точки считаем $\displaystyle w_i = K\left(\frac{\mathrm{dist}(A, t_i)}{h}\right)$, а в условии будет $\displaystyle \sum_{i = 1}^k K\left(\frac{\mathrm{dist}(A, t_i)}{h}\right) I(t_i, 1)$
В качестве ядерной функции могут быть:
- Равномерная функция (Uniform Kernel) \(K(x) = \begin{cases} \frac{1}{2}, & \vert x \vert \leq 1 \\ 0, & \vert x \vert \geq 1\end{cases}\) - то есть все веса равны 1
- Треугольная функция (Triangle Kernel) \(K(x) = \begin{cases}1 - \vert x \vert, & \vert x \vert \leq 1 \\ 0, & \vert x \vert \geq 1\end{cases}\)
- Епанечникова (параболическая) функция \(K(x) = \begin{cases}\frac{3}{4} (1 - x^2), & \vert x \vert \leq 1 \\ 0, & \vert x \vert \geq 1\end{cases}\)
Помимо этого метод $k$-ближайших соседей может использоваться для нахождения регрессии. Тогда предсказанное значение $\hat y$ вычисляется как взвешенное среднее $\displaystyle \frac{\sum_{i = 1}^k w_i y_i}{\sum_{i = 1}^k w_i}$ для $k$ ближайших соседей
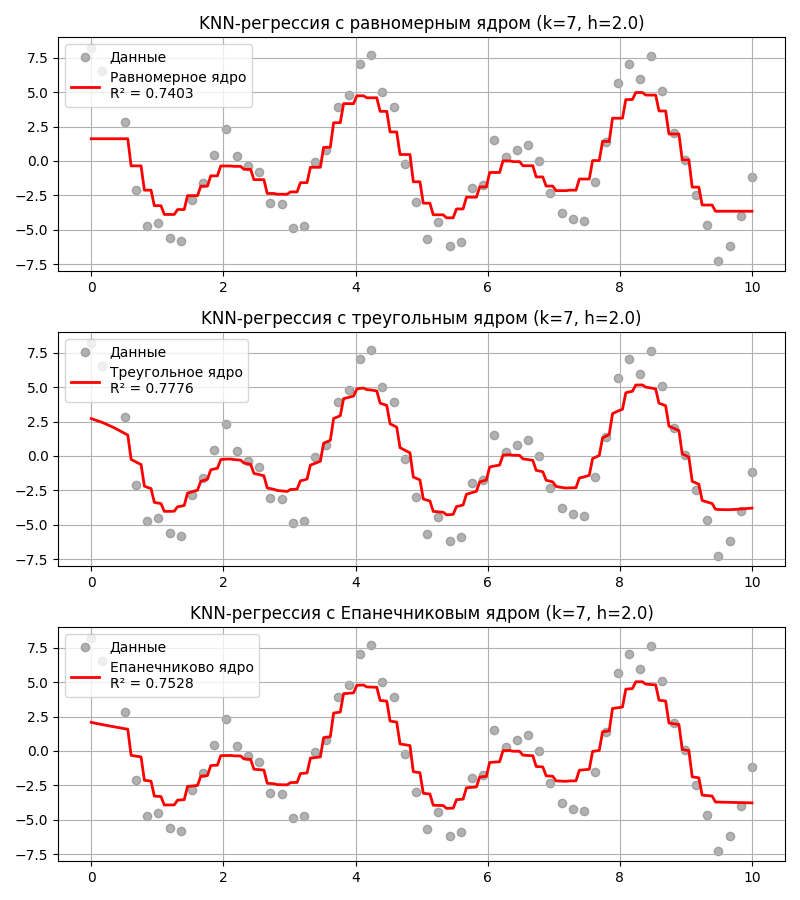
Код примера - machlearn_knn_regression.py
Преимущества метода $k$-ближайших соседей:
- Довольно простой в реализации
- Достаточно точный
- Подходит для классификации и регрессии
Недостатки:
- Неэффективный по памяти - нужно хранить всю выборку (а она может быть размером в несколько тысяч)
- Вычислительно дорогой - $O(nd)$ для вычисления расстояний ($n$ - размер выборки, $d$ - размер переменных), $O(n \log n)$ на сортировку
- Чувствителен к масштабу измерений
- Метрическая близость должна совпадать с близостью по семантическому значению, то есть точки с одним классом должны располагаться рядом
Метод $k$ ближайших соседей позволяет расширить выборку точками, принадлежащих редкому классу - такая техника известна как SMOTE (Synthetic Minority Over-sampling Technique)
Для этого:
- Для точки из редкого класса выбираются $k$ ближайших соседей из того же класса
- Выбирается случайный сосед из этих $k$
- Новая точка создается на отрезке между точкой и этим соседом