itmo_conspects
Лекция 3. Методы понижения размерности, метод главных компонент
Зачастую данные нам данные имеют очень много переменных. Это может привести к “проклятью размерности”:
- Точки становятся разряженными, так как 10-мерный куб заполнять тяжелее, чем 2-мерный квадрат
- Модель становится сложнее, так как нужно учитывать больше признаков
- Алгоритмы, такие как метод k ближайших соседей, становятся сложнее
-
Расстояния становятся относительно близкими
Если рассмотреть расстояние между двумя случайным точками $a$ и $b$ в $k$-мерном кубе $[0, 1]^k$ как случайную величину, то обнаружится, что
-
Матожидание для $(a_i - b_i)^2$ равно $\displaystyle E (a_i - b_i)^2 = \int_0^1 \int_0^1 (x - y)^2 dx dy = \int_0^1 \frac{(x - y)^3}{3} \Big\vert_{x = 0}^{x = 1} dy = \int_0^1 \left(\frac{(1 - y)^3}{3} + \frac{y^3}{3}\right) dy = -\frac{(1 - y)^4}{12} \Big\vert_0^1 + \frac{y^4}{12} \Big\vert_0^1 = \frac{1}{12} + \frac{1}{12} = \frac{1}{6}$
-
$\displaystyle E (a_i - b_i)^4 = \int_0^1 \int_0^1 (x - y)^4 dx dy = \int_0^1 \frac{(x - y)^5}{5} \Big\vert_{x = 0}^{x = 1} dy = \int_0^1 \left(\frac{(1 - y)^5}{5} + \frac{y^5}{5}\right) dy = \frac{1}{30} + \frac{1}{30} = \frac{1}{15}$
-
Дисперсия для $(a_i - b_i)^2$ равна $D (a_i - b_i)^2 = E (a_i - b_i)^4 - (E (a_i - b_i)^2)^2 = \frac{1}{15} - \frac{1}{36} = \frac{7}{180}$
-
Для $\displaystyle \sum_{i = 1}^k (a_i - b_i)^2$ матожидание равно $\frac{k}{6}$, дисперсия - $\frac{7k}{180}$
-
По центральной предельной теореме $\displaystyle \sum_{i = 1}^k (a_i - b_i)^2$ стремится к $N\left(\frac{k}{6}, \frac{7k}{180}\right)$, применяя дельта-метод, получаем, что у случайной величины $\displaystyle \sum_1^k (a_i - b_i)^2$ при $k \to \infty$ матожидание равно $\sqrt{\frac{k}{6}}$, а дисперсия $\left(\left(\sqrt{x}\right)^\prime_{\frac{k}{6}}\right)^2 \cdot \frac{7k}{180} = \frac{6}{4k} \frac{7k}{180} = \frac{7}{120}$
То есть матожидание пропорционально размерности, а дисперсия - нет, поэтому средние расстояния между точками с высоком вероятностью оказываются в окрестности $\sqrt{\frac{k}{6}}$
-
Поэтому нужно уменьшить размерность, не разрушая структуру данных
Существуют несколько методов уменьшения размерности:
- Линейные: PCA, MDS и другие
- Нелинейные: t-SNE, UMAP и другие
Метод главных компонент
Метод главных компонент (Principal Component Analysis, PCA) строится на создании прямых (осей, или главных компонент), которые будут иметь наибольшее отклонение от других осей
Выбирается число этих компонент $n$ - зачастую $n = 2$, так как проще отобразить на графике - и ищутся столько прямых, дисперсия которых максимальна
Для этого:
- Строится матрица ковариаций $D \vec X = {\mathrm{cov} (X_i, X_j)}_{i, j}$
-
Далее для нее находятся собственные числа $\lambda_i$ (такие, что $\lvert (D \vec X) - E \cdot \lambda \rvert = 0$)
Найденные собственные числа показывают долю дисперсии по одной из компонент (умноженную на сумму всех собственных чисел)
-
Берутся $n$ наибольших собственных чисел, для них вычисляются собственные вектора $\vec b$ (такие, что $(D \vec X) \cdot \vec b = \lambda_i \vec b$, при этом $\vec b \neq 0$)
Собственные вектора показывают направления главных компонент. Они сортируются по убыванию по собственному числу, первая компонента (PC1) - это вектор с наибольшим числом, вторая компонента (PC2) - после него и так далее
- Далее формируется матрица проекций, где столбцы - выбранные собственные вектора. Далее вектор из выборки умножается на матрицу проекции и получается точка в новом пространстве
Заметим, что, так как метод главных компонент вычисляет прямые с наибольшим отклонением (то есть дисперсия) от точек, то переменные, имеющие больший диапазон в отличии от других, будут больше влиять на поиск компонент. Поэтому данных перед методом главных компонент нужно стандартизовать
Пример использования PCA: пусть имеется датасет студентов с параметрами hours_studied (среднее время обучения в часах за день), practice_problems (среднее количество решенных задач) и sleep_hours (среднее время сна в часах)
| Номер студента | hours_studied |
practice_problems |
sleep_hours |
|---|---|---|---|
| 0 | 5.80159 | 6.10648 | 7.39829 |
| 1 | 5.16314 | 3.63228 | 9.85228 |
| 2 | 7.01063 | 4.53442 | 7.9865 |
| 3 | 4.65311 | 3.35642 | 6.94229 |
| 4 | 3.17847 | 3.18283 | 8.82254 |
| 5 | 4.92243 | 3.96921 | 6.77916 |
| 6 | 6.05997 | 3.72426 | 8.20886 |
| 7 | 7.23881 | 4.98804 | 6.04033 |
| 8 | 4.16849 | 2.9506 | 6.67181 |
| 9 | 4.4241 | 4.02976 | 8.19686 |
После стандартизации получаем такую матрицу ковариаций:
hours_studied |
practice_problems |
sleep_hours |
|
|---|---|---|---|
hours_studied |
1 | 0.65042 | -0.274431 |
practice_problems |
0.65042 | 1 | -0.241426 |
sleep_hours |
-0.274431 | -0.241426 | 1 |
Для нее находятся собственные числа 2.01551082, 0.93050171 и 0.38732081
Далее находятся собственные вектора:
PC1 |
PC2 |
PC3 |
|
|---|---|---|---|
hours_studied |
0.649822 | 0.258358 | 0.71483 |
practice_problems |
0.640601 | 0.320023 | -0.698008 |
sleep_hours |
-0.409098 | 0.911502 | 0.0424537 |
Получаем матрицу проекций
| 0.649822 | 0.258358 | 0 |
| 0.640601 | 0.320023 | 0 |
| -0.409098 | 0.911502 | 0 |
Далее умножаем вектора из датасета на матрицу, получаем 10 точек на плоскости:
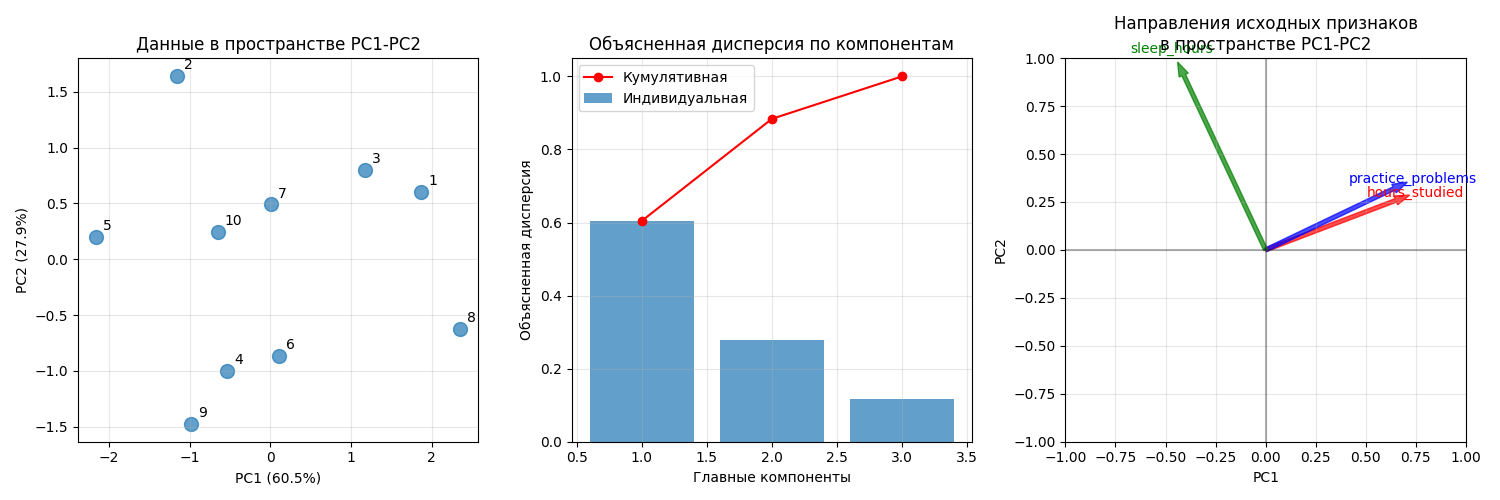
Код примера - machlearn_pca_example.py
Результат PCA часто используется для:
- Визуализации многомерных данных
- Ускорения обучения моделей за счет уменьшения числа признаков
- Подавления шума - последние компоненты часто содержат в основном шум
- Решение проблемы мультиколлинеарности - новые признаки ортогональны
Так как главные компоненты - линейные комбинации исходных признаков, метод главных компонент плохо подходит для нелинейных связей
Для визуализации лучше всего выбрать 2-3 компоненты
Для обучения лучше оставить как можно больше компонент. Для стандартизованных данных можно выбрать столько компонент, для которых собственные числа больше единицы (правило Кайзера) или пока доля объясненной дисперсии не составит не меньше порога (обычно 85%-95%)