itmo_conspects
После данные нужно нормализовать. Нормализация (или масштабирование) данных - приведение их к единому масштабу. Начальные данные могут быть различными единицами измерения. Если не стандартизировать данные, модели машинного обучения станут слишком чувствительны к масштабу признаков, а не к их реальной важности
Методов нормализации существует много, разберем 3 основных:
-
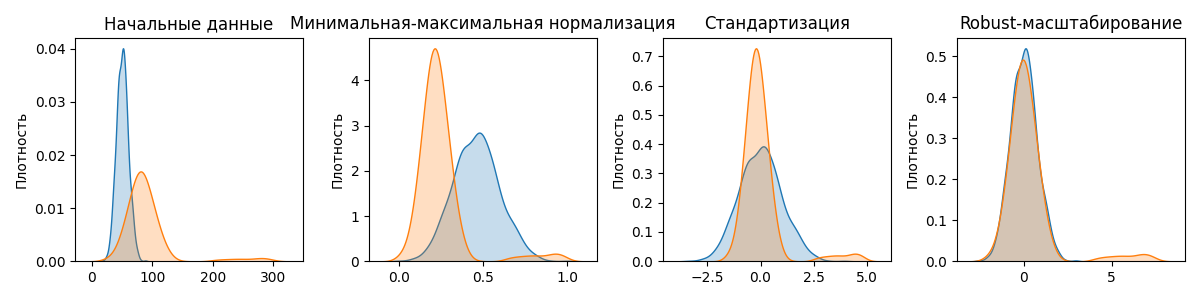
Минимальная-максимальная нормализация
Минимальная-максимальная нормализация - подход, при котором величины в выборке приводятся к диапазону $[0, 1]$. Такая нормализация полезна, если алгоритм принимает числа в некотором диапазоне
\[x_{\text{норм}} = \frac{x - x_{\text{мин}}}{x_{\text{макс}} - x_{\text{мин}}}\] -
Стандартизация
Стандартизация (или Z-масштабирование) преобразует выборка так, что бы среднее было равно 0, а дисперсия - 1:
\[x_{\text{норм}} = \frac{x - \overline{x}}{\sigma_x}\]Выбросы очень сильно влияют на среднее значение выборки, так как изменяют выборочное среднее
-
Robust-масштабирование
Robust-масштабирование (от robust - устойчивый) - метод нормализации, похожий на стандартизацию. Вместо выборочного среднего robust-масштабирование использует устойчивую к выбросам медиану, а вместо отклонения - разницу между 25-ым и 75-ым квантилем
$x_{\text{норм}} = \frac{x - \mathrm{median}(x)}{\mathrm{IQR}(x)}$, где $\mathrm{median}(x)$ - медиана, $\mathrm{IQR}(x)$ - разница между 25-ым и 75-ым квантилем
Также формулу можно представить так: $x_{\text{норм}} = \frac{x - \mathrm{Q_2}(x)}{\mathrm{Q_3}(x) - \mathrm{Q_1}(x)}$, где $\mathrm{Q_1}(x), \mathrm{Q_2}(x), \mathrm{Q_3}(x)$ - квантили выборки уровней $0.25$, $0.5$, $0.75$ соответственно
Примеры работы этих методов:
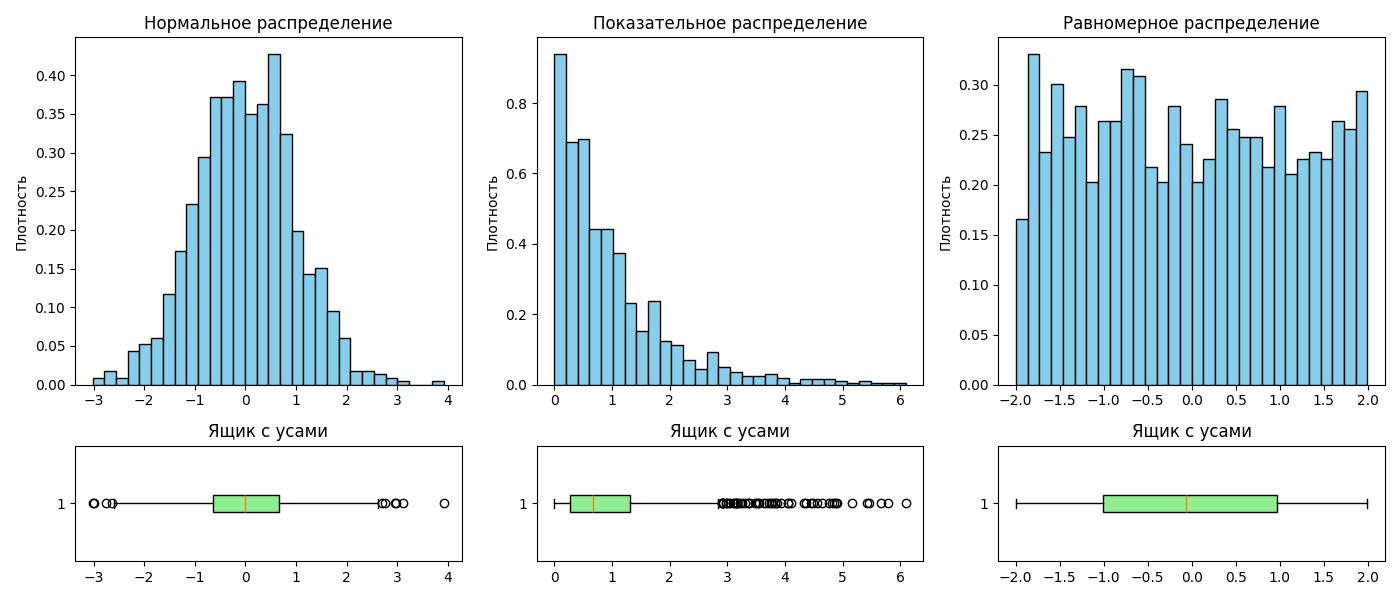
После этого выборку можно наглядно представить в виде гистограммы. При построении гистограммы для ее лучшей читаемости следует помнить, что:
- Столбцы должны быть одинаковой ширины
- Не рекомендуется помещать более двух гистограмм на одной плоскости
- Гистограмма должна занимать все пространство графика
- Высоты столбцов для гистограмм разных выборок должны соответствовать одной оси ординат
Одним из способов визуализации распределения является ящик с усами (или box plot)
Ящик с усами представляет собой прямоугольник, высота которого равна разнице между 25-ым и 75-ым квантилем. Внутри прямоугольника изображается линий, обозначающая медиану
По сторонам прямоугольника располагаются отрезки, так называемые усы. Усы могут строиться как:
- Минимальное и максимальное значения в выборке
- Выборочное среднее $\pm$ стандартное отклонение
- $\text{25-ый квантиль} - 1.5 \cdot \text{разница между 25-ым и 75-ым квантилем}$, аналогично с 75-ым квантилем
- 9-ый и 91-ый квантили
- 2-ой и 98-ой квантили
За пределами усов могут располагать точки, обозначающие выбросы. Ящик с усами позволяет наглядно сравнить распределения:
Лекция 2. Статистические гипотезы
Доверительный интервал уровня $\alpha$ - диапазон значений такой, что вероятность попадания значения в него равна $1 - \alpha$. Интервалы бывают двухсторонними $(a; b)$ и односторонними $(a; +\infty)$
Например, при нормальном распределении почти все значения (99.73%) попадают в доверительный интервал $(a - 3\sigma; a + 3\sigma)$
Статистической гипотезой $H$ называется предположение о распределении наблюдаемой случайной величины. Обычно гипотезы формулируют в паре $H_0$ и $H_1$, где $H_0$ - основная гипотеза, а $H_1$ - альтернативная
Пример: среднее количество лет работы американца до выхода на пенсию равно 64. Нулевой гипотезой будет утверждение “матожидание распределения равно 34”, то есть $H_0 \ : \ \mu = 64$
Гипотезы бывают:
-
левосторонними (left-tailed)
\[\begin{cases} H_0 \ : \ p \geq \alpha \\ H_1 \ : \ p < \alpha \\ \end{cases}\] -
правосторонними (right-tailed)
\[\begin{cases} H_0 \ : \ p \leq \alpha \\ H_1 \ : \ p > \alpha \\ \end{cases}\] -
двусторонними (two-tailed)
\[\begin{cases} H_0 \ : \ p = \alpha \\ H_1 \ : \ p \neq \alpha \\ \end{cases}\]
Гипотеза называется простой, если она однозначно определяет распределение. В другом случае гипотеза называется сложной, и она является объединением конечного или бесконечного числа гипотез
Ошибка первого рода состоит в том, что $H_0$ отклоняется, хотя она верна. Аналогично, ошибка второго рода состоит в том, что $H_1$ отклоняется (то есть $H_0$ принимается), хотя она верна
Вероятность $\alpha$ ошибки первого рода называется уровнем значимости критерия. Вероятность ошибки второго рода обозначаем $\beta$. Мощностью критерия называется вероятность $1 - \beta$ (вероятность недопущения ошибки второго рода)
P-значение (P-value, от probability) - это вероятность (при условии, что нулевая гипотеза верна) получить такое же или более экстремальное значение какой-либо статистики (например, математического ожидания)
Малое p-значение (обычно меньше 0.05) говорит о том, что наблюдаемые данные маловероятны при справедливости основной гипотезы. В таком случае часто отвергают нулевую гипотезу.
Большое p-value означает, что данные согласуются с основной гипотезой, и оснований отвергать её нет
Пример: пусть есть стандартное нормальное распределение и выборка из него. Для выборки нашли среднее и получили $2$
Проверим гипотезу, что математическое ожидание выборки равно $0$:
\[\begin{cases} H_0 \ : \ a = a_0 = 0, & \text{ если } |K| < t_\text{кр} \\ H_1 \ : \ a \neq a_0, & \text{ если } |K| \geq t_\text{кр} \end{cases}\]Здесь $K = \sqrt{n} \frac{\overline{x} - a_0}{\sigma}$ - критерий, а $t_\text{кр}$ - квантиль стандартного нормального распределения уровня $1 - \frac{\alpha}{2}$
Пусть размер выборки $n = 4$, тогда $K = 4$
Вероятность получить выборочное среднее, равное или большее $2$, при условии, что нулевая гипотеза верна (то есть $a = 0$), равна
$P(X \leq -K) + P(X \geq K) = 2 P(|X| \geq K) = 2 (\Phi(+\infty) - \Phi(K)) = 1 - 2 \Phi(K)$
Здесь $P(X \leq a)$ - вероятность того, что случайная величина $X \in N(0, 1)$ будет меньше или равна $a$, $\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_0^x e^{-\frac{z^2}{2}} dz$ - функция Лапласа. Так как тест в гипотезе учитывает модуль, то мы считаем сумму интервалов с двух сторон
Полученное значение называют p-значением. В нашем случае оно равно $0.00008$ - данные маловероятны при такой принятой гипотезе
P-значение не показывает вероятность того, что гипотеза верна или неверна. Также p-значение не говорит о величине эффекта - оно только показывает, насколько данные редки при нулевой гипотезе, но не измеряет силу или практическую важность эффекта, так как зависит от статистики критерия, гипотезы и выборки. Поэтому сравнивать p-значения для разные выборок из разных задач не покажет, какая из них имеет меньшую вероятность на существование
Некоторые часто используемые гипотезы называются тестами:
-
T-тест используется для проверки гипотезы о равенстве матожидания распределения выборки конкретному числу
Пусть дана $\vec X = (X_1, \dots, X_n) \in N(a, \sigma^2)$ с неизвестным матожиданием и дисперсией. Поставим наш критерий $K = \sqrt{n} \frac{\overline{x} - a_0}{S}$, а гипотезу
\[\begin{cases} H_0 \ : \ a = a_0 = 0, & \text{ если } |K| < t_\text{кр} \\ H_1 \ : \ a \neq a_0, & \text{ если } |K| \geq t_\text{кр} \end{cases}\]где $t_\text{кр}$ - квантиль распределения Стьюдента $T_{n - 1}$ уровня $1 - \frac{\alpha}{2}$
Также существует двухвыборочный T-тест (критерий Стьюдента): пусть $(X_1, \dots, X_n)$ и $(Y_1, \dots, Y_m)$ из нормальных распределений $X \in N(a_1, \sigma^2)$ и $Y \in N(a_2, \sigma^2)$
Проверяется $H_0 : a_1 = a_2$ против $H_1 : a_1 \neq a_2$
В качестве статистики возьмем $K = \frac{\overline x - \overline y}{S_p \sqrt{\frac{1}{n} + \frac{1}{m}}}$, где $S^2_p = \frac{(n - 1) S_X^2 + (m - 1) S_Y^2}{n + m - 2}$
Если нулевая гипотеза верна, то при $a_1 = a_2$ получаем, что $K \in T_{n + m - 2}$, если верна альтернативная гипотеза, то $K \longrightarrow \infty$
Критерий: $t_\alpha$ - квантиль $|T_{n + m - 2}|$ уровня $\alpha$
\[\begin{cases} H_0 : a_1 = a_2, & \text{если } K < t_\alpha \\ H_1 : a_1 \neq a_2, & \text{если } K \geq t_\alpha \end{cases}\] -
Критерий знаков используется для проверки гипотезы о медиане распределения выборки
Пусть дана выборка $\vec X = (X_1, \dots, X_n)$, не предполагая нормальности распределения. Проверяется гипотеза о медиане $m$
Считаем количество элементов, больших гипотетической медианы $m_0$: \(S = \text{\#}\{ i : X_i > m_0 \}\)
При нулевой гипотезе $H_0 \ : \ m = m_0$, вероятность того, что наблюдение окажется выше или ниже медианы, равна $\frac{1}{2}$. Следовательно, статистика $S$ имеет биномиальное распределение: $S \in B(n, p = \frac{1}{2}).$
\[\begin{cases} H_0 : m = m_0, & \text{если } 2 \cdot P(S \geq s_\text{набл}) > \alpha, \\ H_1 : m \neq m_0, & \text{если } 2 \cdot P(S \geq s_\text{набл}) \leq \alpha, \end{cases}\]где $s_\text{набл}$ - наблюдаемое значение статистики.
Для больших $n$ биномиальное распределение аппроксимируется нормальным: $S \approx N\left(\frac{n}{2}, \frac{n}{4}\right)$
Тогда используем нормированную статистику $K = \frac{S - n/2}{\sqrt{n}/2}$, и решение гипотезы строится аналогично Z-тесту.
Тогда продолжаем в том же стиле и добавим двухвыборочный критерий знаков:
Аналогично двухвыборочный критерий знаков используется для проверки гипотезы о равенстве медиан двух связанных выборок
Для двухмерной выборки $(X_1, Y_1), \, (X_2, Y_2), \, \dots, \, (X_n, Y_n)$ рассмотрим разности $D_i = X_i - Y_i$
Нулевая гипотеза формулируется как $H_0 : \text{медиана распределения } D_i = 0$, то есть медианы выборок равны.
В качестве статистики берём число положительных разностей: \(S = \text{\#}\{ i : D_i > 0 \}\)
При $H_0$ вероятность знака разности равна $\frac{1}{2}$. Тогда $S \in B(n, \frac{1}{2})$
\[\begin{cases} H_0 : \text{медианы равны}, & \text{если } 2 \cdot P(S \geq s_\text{набл}) > \alpha, \\ H_1 : \text{медианы различаются}, & \text{если } 2 \cdot P(S \geq s_\text{набл}) \leq \alpha, \end{cases}\]где $s_\text{набл}$ - наблюдаемое значение статистики.
Для больших $n$ можно использовать нормальную аппроксимацию: $K = \frac{S - n/2}{\sqrt{n}/2} \approx N(0,1)$
-
Критерий Манна–Уитни (или U-критерий) применяется для проверки гипотезы о равенстве распределений двух независимых выборок
Пусть имеются выборки $X_1, \dots, X_n, \quad Y_1, \dots, Y_m$ из распределений с одинаковой формой, но, возможно, разными сдвигами
Формулируем гипотезы:
\[\begin{cases} H_0 : F_X = F_Y \quad \text{(распределения совпадают)}, \\ H_1 : F_X \neq F_Y \quad \text{(есть сдвиг по медиане)} \end{cases}\]Статистику строим по следующим правилам:
- Объединяем все $n+m$ наблюдений и присваиваем им ранги
- Считаем сумму рангов первой выборки: $R_X = \sum_{i=1}^n r(X_i)$
- Определяем статистику Манна-Уитни: $U = R_X - \frac{n(n+1)}{2}$
При нулевой гипотезе $U$ имеет известное распределение с матожиданием $E U = \frac{nm}{2}, \quad D U = \frac{nm(n+m+1)}{12}$
Для больших выборок берем статистику $Z = \frac{U - nm/2}{\sqrt{nm(n+m+1)/12}} \approx N(0,1)$
\[\begin{cases} H_0 : F_X = F_Y, & \text{если } |Z| < z_{1-\frac{\alpha}{2}}, \\ H_1 : F_X \neq F_Y, & \text{если } |Z| \geq z_{1-\frac{\alpha}{2}}, \end{cases}\]где $z_{1-\frac{\alpha}{2}}$ - квантиль стандартного нормального распределения
Для определения связи между распределениями двух выборок существует понятие корреляции. Коэффициент корреляции $r$ - величина в диапазоне от -1 до 1, показывающая силу и направления связи
-
Коэффициент линейной корреляции (или корреляции Пирсона) измеряет линейную зависимость между случайными величинами из двух выборок
$r = \frac{\mathrm{cov}(X, Y)}{\sigma_x \sigma_y}$
-
Так как связь может быть не строго линейной, существует коэффициент корреляции Спирмана
Для случайной величины $(X_i, Y_i)$ из выборки отдельно считают ранг для $X_i$ и для $Y_i$, далее берется сумма разность рангов для случайных величин из выборки
$\displaystyle \rho = 1 - \frac{6 \sum_i d^2}{n (n^2 - 1)}$, где $d_i$ - разность рангов
Коэффициент корреляции Спирмана показывает монотонную зависимость и основана на рангах, поэтому устойчива к выбросам