itmo_conspects
Лекция 3. Функциональные требования и паттерны
Функциональные требования
При проектировании баз данных надо правильно уметь читать и составлять функциональные требования. Функциональные требования - это такой документ, который формально описывает сущности бизнес-логики, их свойства/связи и действия, которые они совершают или над которыми они совершают
Разберем функциональные требования для аналога Twitter:
- Система должна позволять пользователю зарегистрироваться, указав адрес электронной почты (или номер телефона), имя пользователя и пароль
- При регистрации должна осуществляться валидация введенных данных и отправка подтверждения
- Пользователь должен иметь возможность просматривать и редактировать свой профиль
- Пользователь может подписываться на других пользователей и видеть список своих подписок и подписчиков
- Пользователь должен иметь возможность создавать сообщения (твиты) длиной до 280 символой
- Система должна позволять прикреплять к твитам изображения, видео или ссылки
- После публикации твита пользователь может удалить его (либо неявно скрыть его ото всех)
- Пользователь должен иметь возможность ставить лайки
- Пользователь должен иметь возможность переопубликовать чужие твиты
- Пользователь должен иметь возможность отвечать на твиты
- Пользователь должен иметь возможность искать твиты по ключевым словам и хештегам
- Пользователь может управлять параметрами уведомлений
- Пользователь должен иметь возможность управлять видимостью своих твитов
- Возможность блокировки или ограничения доступа для отдельных пользователей
Нейминг
В PostgreSQL используется snake_case, отношения называются в множественном числе, а атрибуты в единственном.
В первичных и внешних ключах указывается название отношения, чтобы избежать коллизии при объединении отношений, например, user_id и chat_id
Паттерны
Многое-ко-многим
Тривиальной реализацией связи многое-ко-многим будет являться атрибут первого отношения, в котором будут указаны первичные ключи второго отношения (в формате JSON, через запятую или по-другому), однако это будет не оптимально
Правильно будет сделать отдельное отношение с двумя столбцами, в котором первичным ключом будет пара из ключей первого и второго отношений
Вертикальное разделение
Вместо того, чтобы добавлять новые атрибуты в исходное отношение, мы можем создать новое отношение с этим атрибутами. Например:
| user_id | username | |
|---|---|---|
| user_id | big_string | big_binary | biography |
|---|---|---|---|
Если во втором отношении поместить малоиспользуемые атрибуты, то мы получим выигрыш в оптимизации
Фиксированный набор значений
Фиксированный набор значений можно реализовать несколькими способами:
- Ограничение на уровне кода - например, валидация на уровне бекенда
- Перечисление -
ENUMв PostgreSQL - Ограничение -
CONSTRAINTв PostgreSQL - Триггер - обработчик, реагирующий на изменения базы данных
- Справочник - отдельная таблица, которая ремаппит значения; позволяет расширять набор
EAV (Entity-Attribute-Value)
EAV - отношение с тремя атрибутами:
- Entity - уникальный идентификатор объекта
- Attribute - имя атрибута
- Value - его значение
EAV позволяет хранить данные с динамически изменяемой структурой, когда новые атрибуты могут добавлять без необходимости изменения структуры
Полиморфные связи
Допустим, что комментарии можем ставить и на посты, и на картинки. Тогда отношение с комментариями можем представить так:
| comment_id | content | commantable_id | commantable_type |
|---|---|---|---|
Здесь commentable_type определяет, из какого отношения commentable_id будет являться ключом. Однако такой паттерн делает невозможным использование внешнего ключа
Список смежных вершин
Каждый кортеж будет хранить в себе указатель на родителя, тем самым моделируя дерево.
Пример:
| name | id | parent |
|---|---|---|
| food | 1 | null |
| vegetable | 2 | 1 |
| potato | 3 | 2 |
| tomato | 4 | 2 |
| fruit | 5 | 1 |
| apple | 6 | 5 |
| banana | 7 | 5 |
Вложенное множество
Вложенное множество (Nested set) - еще один способ моделирования дерева. Дерево можно представить как вложенное множество:
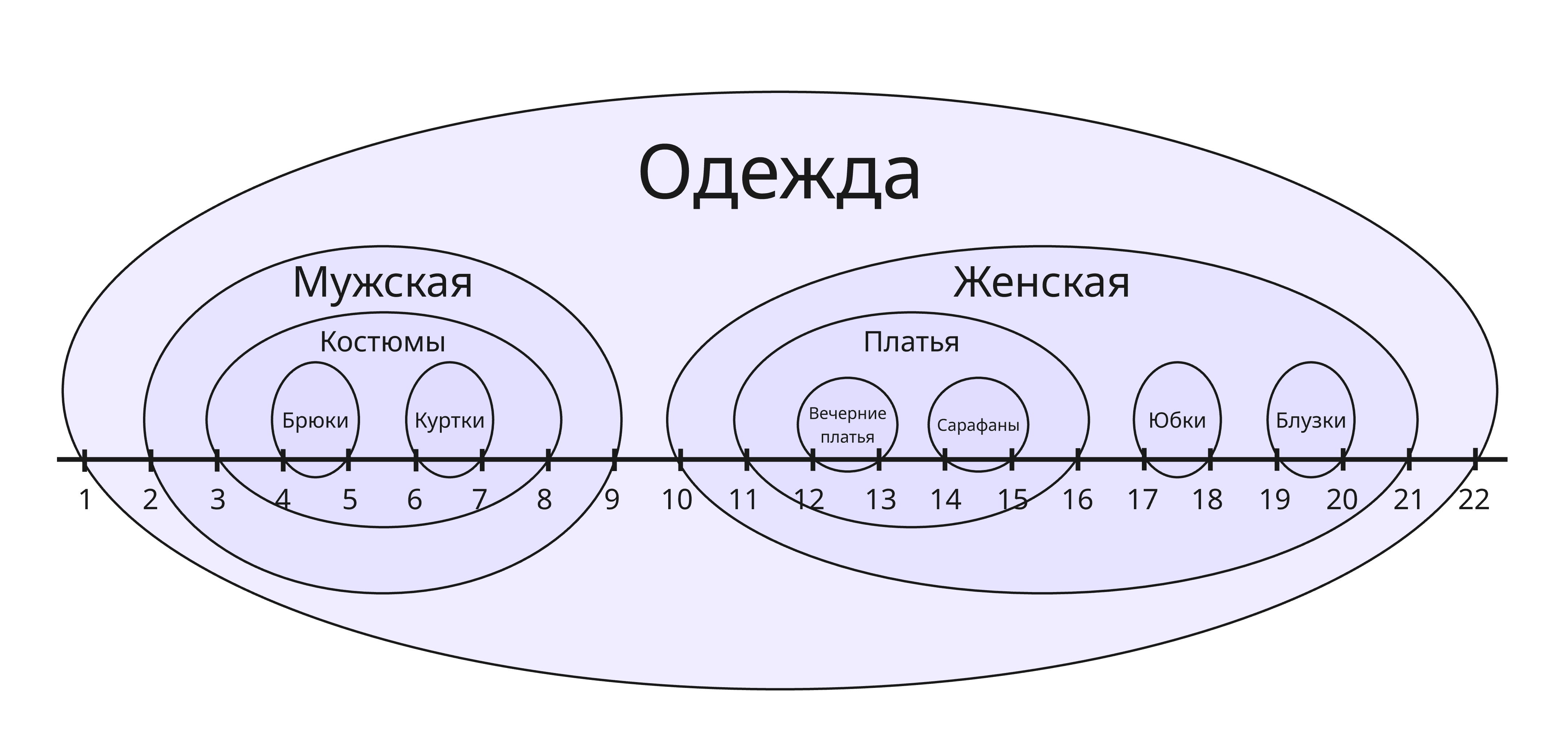
Вместо хранения указателя на родителя, мы будем хранить указатели на левый и правый концы отрезков:
| name | left_end | right_end |
|---|---|---|
| Одежда | 1 | 22 |
| Мужская | 2 | 9 |
| Женская | 10 | 21 |
| Костюмы | 3 | 8 |
| Брюки | 4 | 5 |
| Куртки | 6 | 7 |
| Платья | 11 | 16 |
| Юбки | 17 | 18 |
| Блузки | 19 | 20 |
| Вечерние платья | 12 | 13 |
| Сарафаны | 14 | 15 |
Благодаря этому, мы можем с легкостью определить, является ли какой-либо узел потомком другого узла. Изменять структуру такого дерева - задача нетривиальная, поэтому вложенные множества подойдут для тех деревьев, которые будут чаще всего просматриваемые, нежели изменяемые
Материализованный путь
Материализованный путь (Materialized path) - еще один способ моделирования дерева, в которым для каждого узла мы храним его путь из корня. Например:
| name | path |
|---|---|
| food | 1 |
| vegetable | 1.1 |
| potato | 1.1.1 |
| tomato | 1.1.2 |
| fruit | 1.2 |
| apple | 1.2.1 |
| banana | 1.2.2 |
При помощи инструкции LIKE в SQL мы можем найти всех потомков какого-либо узла. Как и вложенные множества, такой паттерн рекомендуется применять для почти неизменяемых деревьев